au sommaire
Le prix Nobel de physique Paul Dirac avait découvert une nouvelle théorie décrivant un gaz d'électrons à l'aide d'une statistique dite aujourd'hui de Fermi-Dirac. Grâce à elle, Arnold Sommerfeld a fait progresser la compréhension de la conduction des métaux, en attendant les travaux de Félix Bloch et Alan Herries Wilson. Dirac a aussi découvert l'équation décrivant le comportement quantique et relativiste des électrons. Remarquablement, dans le graphène, les électrons de Dirac se comportent comme des fermions de masse nulle. On vient de découvrir des cousins de ces fermions dans un alliage. © AIP, Emilio Sergè Visual Archives
Les tentatives visant à comprendre comment les métauxmétaux et les semi-conducteurs peuvent conduire de l'électricité sont antérieures à la découverte des équations de la mécanique quantique au milieu des années 1920. En effet, les premiers modèles de conduction des électrons dans les métaux sont presque aussi anciens que la découverte de cette particule, puisque c'est en 1900 que Paul Drude a proposé le sien, basé sur une analogieanalogie avec la théorie cinétique des gaz. Pourtant, ce modèle ne permet pas vraiment de comprendre la conductivité des métaux, car il fournit des valeurs bien trop faibles. Ce n'est vraiment qu'avec la découverte des principes de la mécanique quantique, et surtout du caractère ondulatoire de la matièrematière, que des physiciensphysiciens comme Hans Bethe, Rudolph Peierls et quelques autres ont commencé à y voir plus clair.
C'est le prix Nobel de physiquephysique Félix Bloch qui a obtenu la première clé du monde de la physique du solidesolide en utilisant les ondes de matière de Louis de Broglie pour décrire la propagation des électronsélectrons dans un réseau cristallinréseau cristallin. Dans celui-ci, les noyaux occupant les sites du réseau y génèrent un potentiel électrostatiqueélectrostatique effectif variant périodiquement dans l'espace à l'intérieur du cristal. Que ce soit dans un métal ou dans un semi-conducteur, on peut approximer ce potentiel par une série de créneaux. Il existe alors des solutions particulières de l'équation de Schrödingeréquation de Schrödinger contrôlant la propagation des ondes de matière électronique dans ce cristal qui expliquent pourquoi des électrons peuvent s'y déplacer sans être rapidement freinés par des collisions avec les noyaux. Ces solutions décrivent ce que l'on appelle des ondes de Bloch.

Félix Bloch (1905-1983) était un physicien suisse. Edward Mills Purcell et lui se sont partagé le prix Nobel de physique de 1952 pour leurs travaux sur la résonance magnétique nucléaire (RMN). On lui doit d'importants travaux en physique du solide avec la découverte des fameuses ondes de Bloch. © Weizmann Institute of Science
Des ondes de Bloch aux bandes d'énergies
Remarquablement, de même que de la lumièrelumière ne se déplace pas à la même vitessevitesse dans un milieu d'indice n que dans le vide, tout se passe comme si la massemasse « effective » des électrons changeait en fonction de la nature du cristal considéré, en raison de l'existence de ces ondes de Bloch. Dans certains cas, elle peut même apparaître comme négative et dépendre de la direction de propagation des ondes.
Comme l'a montré en 1931 le physicien Alan Herries Wilson, les ondes de Bloch conduisent à l'existence de niveaux d'énergieénergie si serrés qu'ils se comportent comme des bandes d'énergie continues pouvant être occupées par des électrons, différant des niveaux d'énergie principaux, bien distincts, qui existent dans des atomes. On distingue alors une bande de valencebande de valence dans laquelle les électrons ne peuvent participer à des mouvementsmouvements de conduction, et une bande de conductionbande de conduction qui autorise ces mouvements.
Comme on peut le voir sur le schéma ci-dessous, lorsque ces deux bandes sont largement séparées, les électrons restent dans la bande de valence et on a un isolant. Lorsque ces deux bandes se recouvrent partiellement, on a un conducteur. Lorsqu'elles sont séparées par un faible intervalle d'énergie (on parle de gapgap en anglais), on a affaire à un semi-conducteur, car il est possible de faire passer, sous certaines conditions, des électrons de la bande de valence à la bande de conduction.
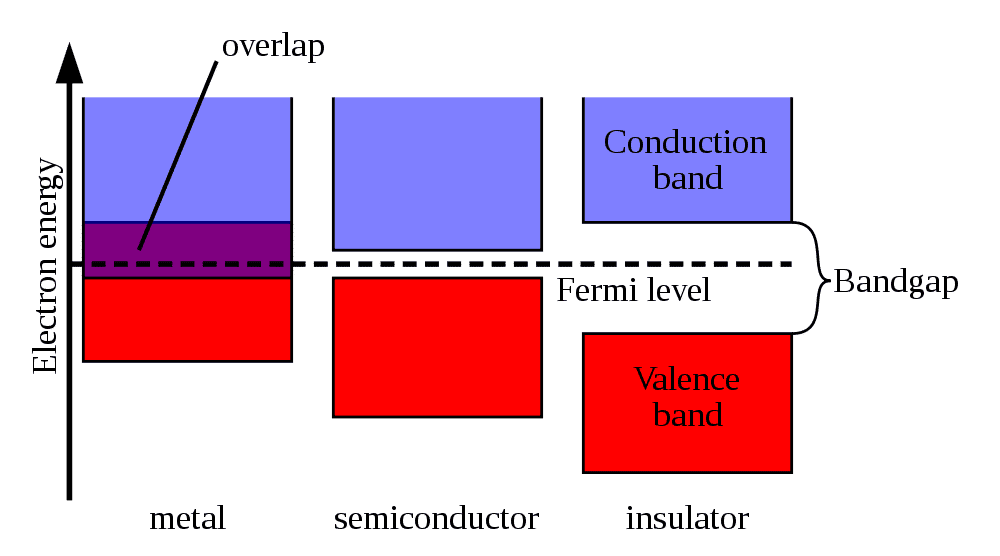
Sur ce schéma, on a représenté les bandes de conduction et de valence dans un solide (en abscisse, l’énergie des électrons qui peuvent occuper ces bandes). On voit la différence entre, de gauche à droite, un conducteur (metal), un semi-conducteur (semiconductor) et un isolant (insulator). © Pieter Kuiper, Wikipédia , DP
Masse effective nulle pour des électrons dans le HgCdTe
Il est possible de développer une théorie quantique fine tenant compte de différents phénomènes, comme l'existence du spinspin des électrons, pour comprendre plus en détail comment se fait la conduction dans les solides à partir des ondes de Bloch et de l'existence des bandes d'énergie. On l'utilise lorsqu'on veut chercher à créer des composants pour l'électronique et l'optronique doués de propriétés bien particulières. Depuis 1957, il existe notamment une théorie célèbre, dite aussi modèle de Kane (du nom du physicien Evan O. Kane qui l'a proposé), qui décrit en détail le couplage entre la bande de conduction et la bande de valence. Elle permet de calculer la masse effective des électrons dans un solide cristallin.
Une équipe internationale de chercheurs français, russes et allemands vient de vérifier une des prédictions de cette théorie : l'existence d'électrons de masse effective nulle dans un cristal 3D de tellurure de mercuremercure-cadmiumcadmium (HgCdTe), avec une structure de type zinczinc-blendeblende. L'article qu'ils ont publié dans Nature à ce sujet est en accès libre sur arxiv.
Théorie quantique de la conduction et fermions de Kane
Ce n'est pas la première fois que l'on observe la propagation d'électrons doués d'une masse effective nulle dans un solide, mais jusqu'à présent, le phénomène restait confiné à des objets dont on pouvait considérer qu'ils avaient une structure en 2D, comme le graphènegraphène et les nanotubes de carbone, qui sont eux-mêmes des feuillets de graphène enroulés. Pour distinguer les électrons effectifs dans le graphène de ceux dans le cristal de HgCdTe, les physiciens ont baptisé les seconds fermionsfermions de Kane, alors que les premiers sont des fermions de Dirac.
L'apparition des fermions de Kane dans un cristal de HgCdTe était soupçonnée dès les années 1960. Malheureusement, la technologie du XXe siècle n'était pas encore suffisamment avancée pour le fabriquer. Il fallut attendre des progrès récents dans la technique d'épitaxie par jet moléculaire. On pense que cet alliagealliage devrait pouvoir conduire à de nouveaux dispositifs en optoélectroniqueoptoélectronique.