au sommaire

Andreï Okounkov
Groupes symétriques et groupe S(∞)
Dès le début du XIXème siècle, Lagrange et Galois, entre autres, avaient reconnu le rôle central que jouent les ensembles de permutation en mathématiques : les premiers travaux d'A. Okounkov portent sur un type de généralisation de ces groupes. Une fois n'est pas coutume, une permutation correspond bien à l'idée que l'on s'en fait : c'est simplement un réarrangement, qui s'écrit traditionnellement sous la forme d'un tableau en repérant les positions initiales et finales des objets (en l'occurrence, des cubes de couleurs sur la figure).
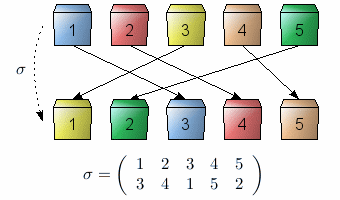
Permutation d'un ensemble à 5 éléments et son écriture mathématique.
Crédits : S. Tummarello.
L'ensemble des permutations d'un ensemble jouit d'une structure algébrique remarquable : c'est un groupe, ce qui veut dire qu'il est possible de composer deux permutations pour en obtenir une nouvelle (en les appliquant successivement - voir figure), et qu'en outre il est possible de revenir à la configuration initiale par une permutation dite « inverse ». L'ensemble des permutations d'une collection de n objets porteporte le nom de groupe symétrique d'ordre n.
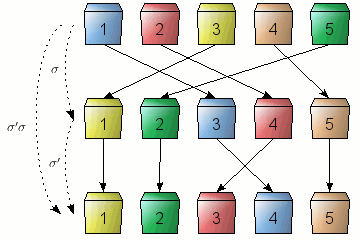
Composition σ'σ de deux permutations σ et σ'.
Crédits : S. Tummarello.
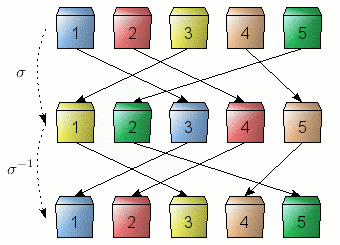
Inverse σ-1 d'une permutation σ.
Crédits : S. Tummarello.
Pour définir le groupe S(∞) sur lequel a travaillé A. Okounkov, il faut s'imaginer les permutations d'un ensemble infini (typiquement l'ensemble des entiers positifs : 1, 2, 3, etc.) qui n'intervertissent qu'un nombre fini (mais quelconque) d'éléments.
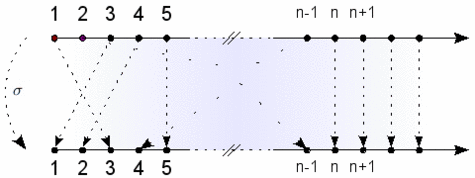
Illustration de l'action d'un élément σ de S(∞) sur les entiers positifs : au-delà d'un certain rang n, les objets ne sont pas dérangés.
Crédits : S. Tummarello.
Représentation des groupes
Au XXème siècle, les mathématiciensmathématiciens se sont intéressés aux différentes manières de représenter géométriquement un groupe quelconque. Par exemple le groupe symétrique d'ordre 3 peut se voir comme les isométries du plan qui laissent invariants les sommets d'un triangle équilatéral. Mais pour un groupe donné, il existe beaucoup de représentations possibles, l'espace de représentation pouvant être le plan comme précédemment, mais le plus souvent un espace de dimension quelconque, voire infini (espaces de Hilbert). Toutefois parmi toutes ces représentations, seules quelques-unes en constituent en quelque sorte les briques élémentaires : ce sont les représentations irréductibles.
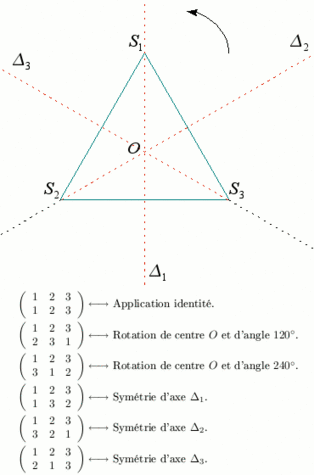
Une représentation du groupe symétrique d'ordre 3 en tant que symétries d'un triangle équilatéral, et le dictionnaire associé : à chaque permutation correspond une isométrie du plan qui permute les sommets.
Crédits : S. Tummarello.
A. Okounkov a ainsi travaillé sur l'étude des représentations irréductibles du groupe S(∞), entamée en 1964 par E. Thoma. S(∞) est cependant un des exemples de "groupe sauvage", ce qui signifie, selon les mots d'A. Okounkov, "qu'il n'apparaît pas raisonnable d'étudier toutes les représentations irréductibles de ce groupe1
". Dans sa thèse de doctorat, A. Okounkov donne néanmoins une méthode pour construire toutes les représentations irréductibles d'un certain type (dites "admissibles") du groupe S(∞) et il démontre plus tard à ce sujet une conjecture due à G. Olshanski (dont l'énoncé est trop technique pour apparaître ici).
Les partitions aléatoires
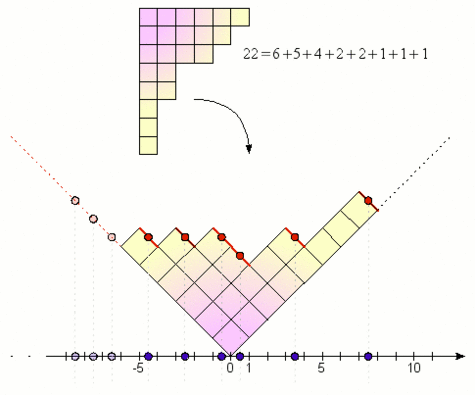
Propriété frappante des groupes symétriques, leurs représentations irréductibles sont liées aux différentes écritures possibles de l'ordre n comme sommes d'entiers non-nuls et décroissants, appelées "partitionspartitions". Par exemple le nombre 5 admet sept partitions et il y a ainsi exactement sept représentations irrédutibles du groupe symétrique d'ordre 5. Chacune de ces partitions se visualise graphiquement par un "diagramme de Young" dont les lignes donnent les termes de la décomposition.
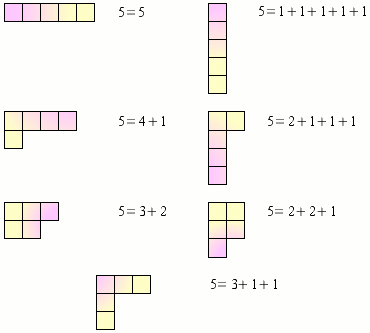
Les sept partitions de l'entier 5 et les diagrammes de Young associés : à chacun de ces diagrammes correspond une représentation irréductible du groupe symétrique d'ordre 5, qui en compte donc sept au total.
Crédits : S. Tummarello.
L'étude des réprésentations irréductibles du groupe S(∞) a conduit A. Okounkov à considérer le problème dans sa globalité : si l'on choisit au hasard des partitions pour des entiers n de plus en plus grands, leurs diagrammes de Young présentent en effet des régularités de plus en plus prononcées. Il existe en particulier une mesure de probabilité, appelée mesure de Plancherel (par analogieanalogie avec la théorie de Fourier), qui traduit en substance l'allure typique des diagrammes de Young.

Les 42 diagrammes de Young pour n=10 et leur superposition : le niveau de gris indique pour chaque case sa probabilité d'occurence parmi tous les diagrammes (mesure de Plancherel). A titre d'exemple, cette probabilité vaut 19/42 pour la case entourée en rouge.
Crédits : S. Tummarello.

Superposition des 5 604 diagrammes de Young pour n=30.
Crédits : S. Tummarello.
Dans la même veine, A. Vershik et S. Kerov avaient déjà montré à la fin des années 70 que la « ligne d'horizon » des diagrammes de Young est à la limite une courbe relativement simple, dont l'équation s'écrit :
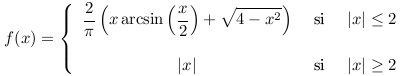
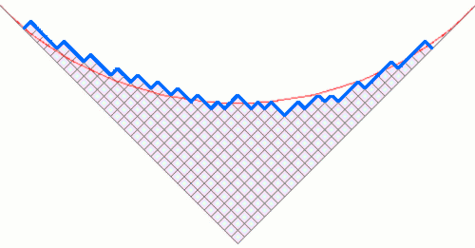
" Ligne d'horizon " (en bleu) d'un diagramme de Young " typique " et la courbe limite de Vershik-Kerov (en rouge).
Crédits : S. Tummarello.
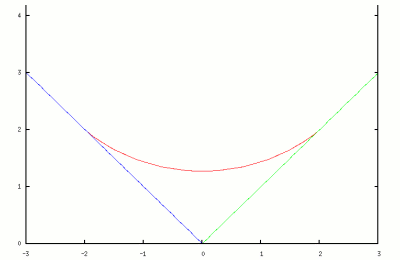
Courbe limite de Vershik-Kerov obtenue à l'aide du logiciel " gnuplot ".
Les nouvelles techniques introduites par A. Okounkov pour explorer la théorie de ces partitions aléatoires forment la clé de voûte de ses premiers travaux. Sa démonstration de la conjecture de Baik-Deift-Johansson en est une remarquable illustration. De manière très grossière, on peut obtenir une sorte de carte d'identité d'un diagramme de Young en le projetant convenablement sur une droite graduée : J. Baik, P. Deift, et K. Johansson avaient pressenti qu'il est possible de mettre en relation ces cartes d'identité avec les signatures (l'ensemble des valeurs propres) de certaines matrices aléatoires2 quand leur taille augmente : A. Okounkov a établi cette correspondance en 1999.
L'ensemble des points bleus forme la carte d'identité de ce diagramme de Young.
Crédits : S. Tummarello.
A. Okounkov : un mathématicien généreux
Les matrices aléatoires sont un sujet d'importance en physique, notamment pour les théories de gravité quantique (théories des cordesthéories des cordes) et la supersymétriesupersymétrie. Mais les apports d'A. Okounkov à la physique théorique s'étendent bien au-delà, avec par exemple la description complète des " invariants de Gromov-Witten ", qui dénombrent (via la cohomologie) les points d'intersection d'une courbe avec des objets géométriques complexes (comme par exemple les variétés de Calabi-Yau, qui jouent un rôle essentiel dans les théories des cordes).
A. Okounkov a également apporté des contributions majeures visant à unifier la physique théorique, en pleine activité aujourd'hui : son étude de la "cohomologie quantique des schémas de Hilbert" lui a notamment permis de conjecturer des correspondances entre deux théories de nature assez différente (à savoir celles de Gromov-Witten et de Donaldson-Thomas).
L'œuvre de A. Okounkov concernent par ailleurs des sujets aussi variés qu'importants tels que la physique des cristaux, les diagrammes de phasediagrammes de phase3, les courbes elliptiques, la géométrie algébrique... Face à une telle somme de résultats, il n'est guère possible à l'auteur de cet article de les évoquer4 tous. Aussi, en guise de conclusion, citons le lauréat au sujet de l'interaction entre les probabilités et les théories des cordes et de supersymétrie : "ce domaine regorge de questions encore largement ouvertes, et selon moi il déborde de nombreux phénomènes nouveaux qui n'attendent que d'être découverts5
"...
1. "The study of all irreducible representations of S(∞) does not seem to be a reasonable problem
". A. Okounkov, On the representation of the infinite symmetric group, 1998, p. 2.
2. Une matrice aléatoire est un tableau dont les éléments sont des variables aléatoires.
3. Les diagrammes de phase décrivent l'état de la matièreétat de la matière (liquideliquide, solidesolide ou gazeuse) en fonction de paramètres la décrivant (température, pressionpression, etc.).
4. Ni de les comprendre !
5."The field is still full of wide open questions and, in my opinion, it is also full of new phenomena waiting to be discovered
". A. Okounkov, Random partitions and instanton counting, 2006, p. 22.






















