Energie de liaison

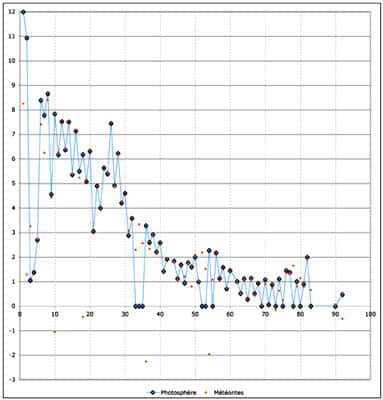
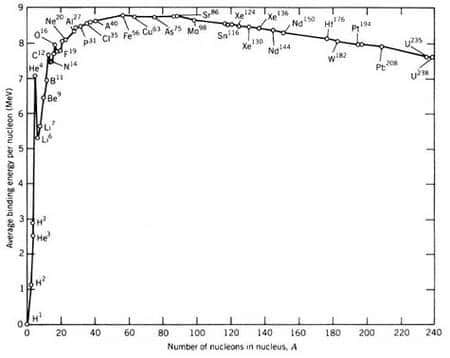
Puisque de l'énergie est libérée par l'assemblage des nucléons, pourquoi tous les nucléons de l'univers ne se rassemblent-ils pas en un noyau gigantesque ? Pour le comprendre, et pour comprendre ce qui se passe dans un noyau, Aston a tracé la courbe mesurant l'énergie de liaison des noyaux en fonction de leur (nombre de) masse A, ou plus exactement l'énergie de liaison par nucléon E/A.

Courbe d’Aston © NASA-GSFC

Cette courbe est très riche d'enseignements : qu'y voit-on en effet ? D'abord E/A est à peu près constante, de l'ordre de 8 MeV pour la plupart des noyaux. C'est trop peu pour augmenter le nombre total de nucléons (il faut 940 MeV pour créer un nucléon), mais assez pour transformer un proton en neutronneutron, et inversement. Ensuite on note que E/A augmente jusqu'à A ~ 50 (la position du ferfer et du nickelnickel) avant de diminuer ensuite peu à peu. Enfin on remarque quelques à-coups, certains noyaux apparaissant plus liés que la « normale », en particulier l'héliumhélium et certains noyaux ayant à la fois un nombre pair de protons et un nombre pair de neutrons comme le carbonecarbone 12 ou l'oxygèneoxygène 16.

La forme de la courbe d'Aston s'explique à peu près bien, comme Bethe et Weizsäcker l'ont montré en 1935, en additionnant plusieurs contributions simples. Tout d'abord, chaque fois qu'un nucléon se colle aux autres, une quinzaine de MeV d'énergie de liaison sont libérés, d'où une première contribution a_V ~ 15  MeV.

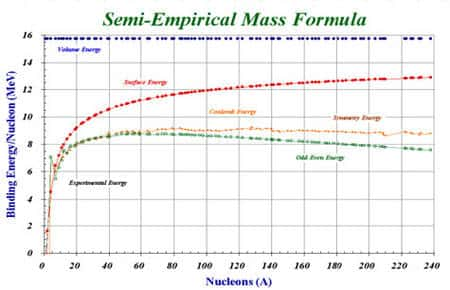
Les différentes contributions à la courbe d’Aston

Mais bien sûr, les nucléons sont moins liés quand ils sont proches de la surface que lorsqu'ils sont enfouis à l'intérieur, puisqu'ils ont moins de voisins. L'énergie de liaison par nucléon est diminuée d'un terme -a_SA^2/3, proportionnel à la surface. Le coefficient aS est aussi de l'ordre de 15 MeV, l'effet est donc important pour les petits noyaux.

Une deuxième complication vient de la mécanique quantiquemécanique quantique. Comme les électronsélectrons dans l'atomeatome, les nucléons du noyau ne peuvent posséder que des énergies définies (c'est la quantificationquantification) formant une suite de niveaux d'énergie croissante, les couches. Les protons comme les neutrons sont des fermionsfermions, et deux fermions ne peuvent pas occuper le même état quantique (principe d'exclusion de Pauliprincipe d'exclusion de Pauli). Les niveaux de plus basse énergie sont occupés les premiers, mais après il faut bien occuper les niveaux plus élevés. Heureusement, protons et neutrons sont différents, et ils ont chacun leurs propres niveaux d'énergie, et il est donc énergétiquement préférable de remplir en parallèle les deux séries, et donc d'avoir à peu près autant de protons que de neutrons. Ceci se traduit par une « pénalité » -a_A(N-Z)²/A avec un coefficient a_A ~ 20 MeV : un excès de protons ou de neutrons entraîne donc une lourde pénalité, à tel point qu'il vient vite un moment où les protons ou neutrons « en trop » ne sont pas liés, et ils sont immédiatement perdus par le noyau.

Une troisième complication vient de la charge électrique des protons : leur répulsion électrique induit une pénalité coulombienne -a_CZ²/A^1/3  proportionnelle au carré de la charge électrique Z. Le coefficient a_C ~ 0.6 MeV semble petit, mais il finit par dominer pour Z>50. Il est possible d'alléger cette pénalité en augmentant le nombre de neutrons, qui apportent plus de colle sans créer de répulsion.  Mais ce n'est qu'un palliatifpalliatif temporaire puisque l'attraction est proportionnelle au nombre A de nucléons alors que la répulsion augmente comme le carré de la charge Z et finit par l'emporter.

Il y a une quatrième complication, d'origine quantique elle aussi : protons (et neutrons) minimisent leur énergie en s'appariant (par paires de spinsspins inverses) et les noyaux pairs-pairs sont donc plus stables que les pairs-impairs et que les impairs-impairs. Cela se paramétrise par un bonus ou une pénalité d'appariement ±δ(A,Z). On a remarqué également que les noyaux étaient particulièrement stables quand ils possédaient certains nombres, dits « magiques », de protons ou de neutrons : 8, 20, 28, 50, 82, 126, 184,nombres  dont l'origine est à peu près, mais pas complètement, comprise.
En recollant les morceaux, nous avons l'équationéquation de Bethe et Weizsäcker pour l'énergie de liaison par nucléon : E/A = a_V -a_SA^2/3 -a_A(N-Z)²/A -a_CZ₂/A ^/3  ±δ(A,Z) .

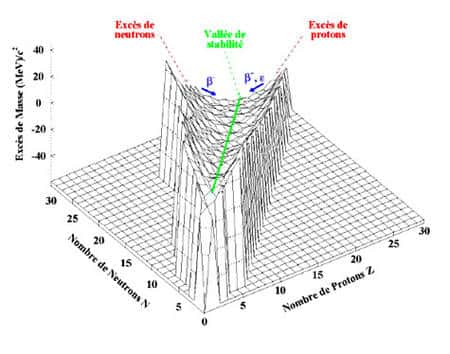
Mais nous avons maintenant bien plus qu'une explication de la courbe E(A) d'Aston, nous avons une estimation de l'énergie de liaison de n'importe quel noyau, quelle que soit son nombre Z de protons et N de neutrons. Nous pouvons alors tracer la carte des noyaux possibles en portant cette énergie de liaison en fonction de Z et de N. Cela nous donne une sorte de paysage dont le relief représente cette énergie de liaison, les creux correspondant aux noyaux les plus liés, les pics aux noyaux les moins liés. Minimiser l'énergie correspond à rechercher les creux les plus profonds de ce paysage. Nous avons déjà remarqué qu'il ne peut pas y avoir d'excès considérable de protons ou de neutrons, et qu'il ne peut pas non plus y avoir de noyau très lourd en raison de la répulsion électrique. Les 3000 à 5000 noyaux possibles s'alignent donc le long d'une courbe qui suit N=Z au début avant de s'infléchir peu à peu.

La formule de Bethe et Weizsäcker indique ensuite que l'énergie de liaison, pour un nombre de massenombre de masse A donné, est quadratique en Z : cela implique que cette énergie est minimale pour une valeur précise de Z et qu'elle augmente si Z s'écarte, en plus ou un moins, de chaque côté. Dans notre paysage, nous avons donc une vallée parabolique dont le fond suit la valeur optimale de Z pour A (et donc N=A-Z) donné. On l'appelle la vallée de stabilité.

Mais non seulement le nombre de noyaux possibles est limité, la plupart d'entre eux disparaissent en quelques secondes : ils sont instables, radioactifs. Mais pourquoi ?

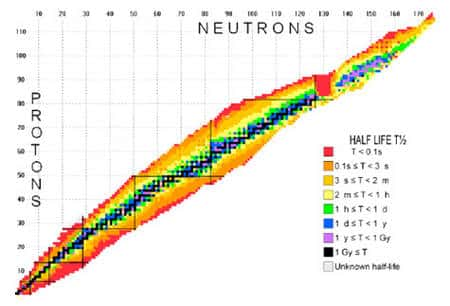
Carte des noyaux connus, la couleur indiquant leur durée de vie © Nubase