au sommaire
À n'en pas douter, la fonction d'onde Ψ de Schrödinger a jeté un pavé dans la mare du réel des physiciensphysiciens. Sa complexité ne réside pas seulement dans son étrange signification et ce qu'elle permet de prévoir par le calcul, mais aussi et surtout dans le fait que c'est une fonction à valeurs complexes.
Si les mathématiciensmathématiciens n'avaient pas déjà inventé les nombres complexes, les physiciens auraient dû les définir avant de pouvoir envisager de construire la théorie quantique, tout en piochant dans la théorie des groupes qui, elle aussi, serait bien en peine sans les complexes.
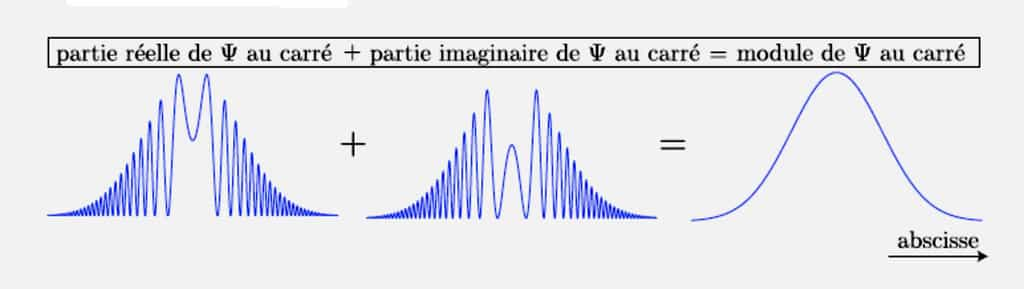
Le caractère incontournable de la complexité de Ψ saute aux yeuxyeux à la simple vision des équations fondamentales où i (i2 = -1) trône sans crainte d'être déboulonné, que ce soit celle de Schrödinger ou celle de Heisenberg, Born et Jordan. Il se mesure aussi tout bêtement en dessinant dans un cas simple les parties réelle et imaginaire de Ψ, et son module carré. On voit comment les deux premières, variant à toute vitesse, se conjuguent (!) pour reconstituer une bosse de probabilité qui, certes, n'est pas l'image naïve que l'on se fait d'une particule, mais commence quand même diablement à y ressembler (voir la figure ci-dessous, extraite de Mécanique quantique, tome I de Claude AslangulClaude Aslangul, De Boeck, Bruxelles, 2007).
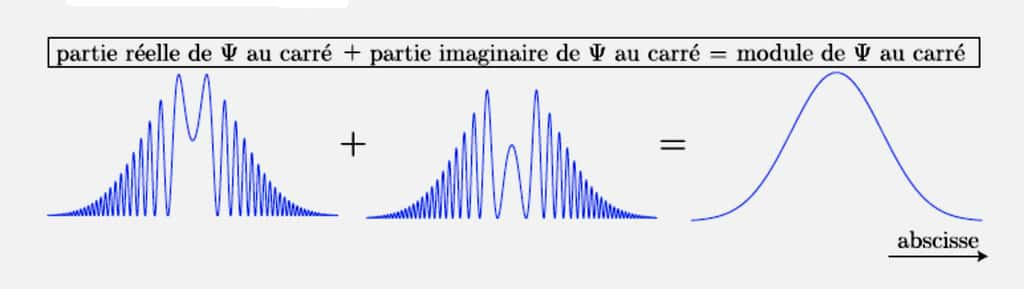
Exemple montrant comment les parties réelle (à gauche) et imaginaire (au centre) de Ψ se donnent la main pour former un joli paquet d'ondes (à droite). © Claude Aslangul
Il arrive, c'est vrai, que la fonction d'onde soit à valeurs réelles, mais ce sont des cas très particuliers qui ne doivent pas égarer. Sans les complexes, pas d'amplitude de probabilité, pas d'interférences, pas de relations d'incertitude. Bref, plus rien de ce qui fait l'essence même de la théorie quantique.
Cela bouscule sans doute les habitudes, mais comme l'a dit Sophus Lie, « si la vie est complexe, c'est parce qu'elle a une partie réelle et une partie imaginaire ».