au sommaire
Initialement proposée par Gabriele Veneziano à la fin des années 1960 pour décrire les forces nucléaires fortes, la théorie des cordes est devenue au début des années 1970 et surtout 1980 le meilleur espoir d'obtenir une théorie unifiée des champs de force et des particules de matière dans l'univers. Il s'agit également d'une piste pour réconcilier les lois de la mécanique quantique avec celle de la relativité générale.
C'est Leonard Susskind et indépendamment Yoichiro Nambu qui ont compris que la théorie développée à partir des travaux de Veneziano revenait à remplacer les particules par des cordes vibrantes. Ces cordes, ouvertes ou fermées, peuvent vibrer et tourner, ce qui veut dire qu'elles peuvent contenir de l'énergieénergie, et donc avoir une massemasse et posséder un moment cinétiquemoment cinétique.
Pendant les années 1970, plusieurs chercheurs découvrirent alors que si l'on voulait que ces cordes respectent les lois de la relativité restreinterelativité restreinte et de la mécanique quantique, elles devenaient capables de représenter des particules de différents spinsspins et masses, comme les quarksquarks, les leptonsleptons et les bosonsbosons associés aux forces du cosmoscosmos comme les gluonsgluons, le photonphoton et le graviton.
Des dimensions spatiales supplémentaires
Le prix à payer était d'admettre que l'espace-tempsespace-temps où évoluent ces particules possédait en fait non pas 4 mais 10 ou 11 dimensions, et qu'une nouvelle et puissante symétrie naturellement associée à la géométrie de l'espace-temps, la supersymétrie, dictait d'autres propriétés de ces cordes. On obtenait alors à partir d'un seul objet, une corde, les équationséquations des champs de Yang-Millschamps de Yang-Mills du modèle standardmodèle standard des interactions ainsi que les équations de la relativité générale d'EinsteinEinstein.
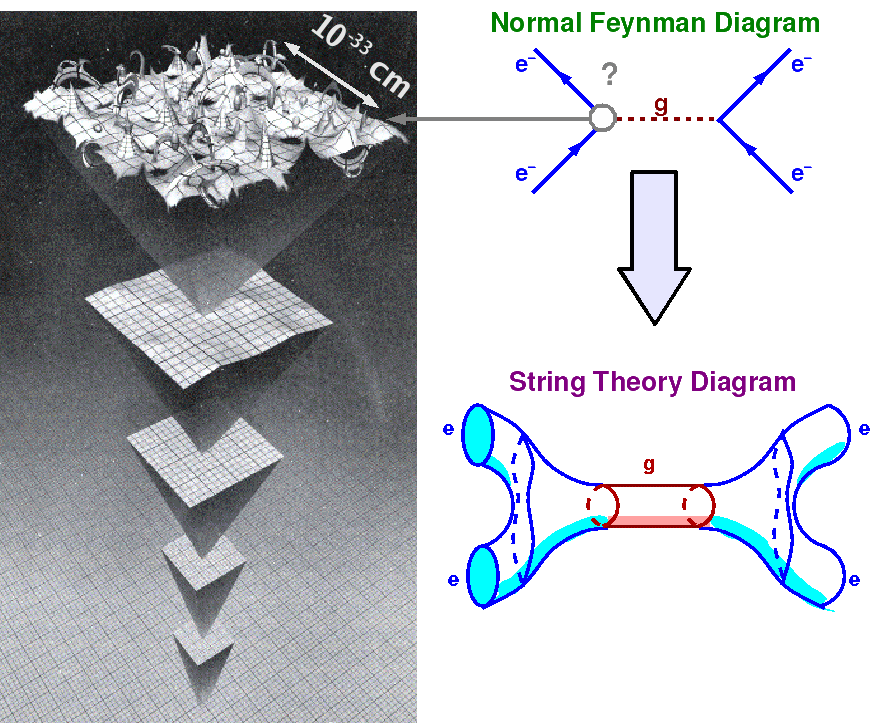
La théorie des cordes est l'une des deux principales théories de gravitation quantique. Elle permet de décrire l'espace-temps fluctuant à l'échelle de Planck (10-33 cm, à gauche de l’image). Elle permet aussi de décrire la théorie quantique des champs de force, comme la QED gouvernant les interactions entre électrons, en remplaçant les particules des diagrammes de Feynman (en haut à droite) par des cordes vibrantes, ouvertes ou fermées, balayant des surfaces dans l'espace-temps (en bas à droite). © Indiana University
Des généralisations des diagrammes de Feynmandiagrammes de Feynman avec des cordes balayant des surfaces et non plus des lignes dans l'espace-temps se montraient alors capables de faire des calculs quantiques avec le champ de gravitationgravitation libre des problèmes de divergences infinies rencontrés en gravitation quantique, et d'éliminer ce qu'on appelle des anomalies avec les champs de Yang-Mills.
Les six dimensions spatiales supplémentaires exigées par la théorie des cordes des années 1980, devenue théorie des supercordes du fait de la présence de la supersymétriesupersymétrie, faisaient revivre les fameuses théories de Kaluza-Klein des années 1930 et 1960.
De la supergravité en 11 dimensions à la théorie M
Le milieu des années 1990 fut marqué par une révolution dans la théorie des supercordes. Avec des chercheurs comme Joseph Polchinski et Edward Witten, on se rendit compte que la théorie des supercordes contenait aussi des objets non plus sous forme de filaments, mais de membranes et même de volumesvolumes, et que sa véritable nature se cachait dans un espace-temps avec sept dimensions spatiales supplémentaires. La théorie des supercordes devenait alors une manifestation d'une théorie en 11 dimensions d'espace-temps et se réduisant, à basse énergie dans cet espace, à une pure théorie de supergravité.
Cette nouvelle théorie des supercordes, baptisée théorie Mthéorie M, est toujours en chantier actuellement. Elle a permis de comprendre l'origine de l'entropieentropie des trous noirs, de jeter quelques lumièreslumières sur la supraconductivité à haute température et l'énergie noireénergie noire, mais ne permet toujours pas de retrouver les masses des particules et divers autres paramètres du modèle standard.
Pour en savoir plus sur la théorie des supercordes, la théorie M et leur histoire, on peut consulter le site DiffusionDiffusion des savoirs de l'École normale supérieure.

























