Particules de matière noire supersymétriques et monopôles magnétiques, que dit le LHC ?

Si le LHC au Cern a d'abord été conçu pour découvrir le boson de Brout-Englert-Higgs (BEH) et étudier la façon dont ce boson est à l’origine des masses de plusieurs particules fondamentales, il est également apparu rapidement que le LHC avec ses détecteurs géants, en particulier Atlas et CMSCMS, pouvait servir à chasser de la nouvelle physique.

En fait, encore au début des années 2000, la majorité des membres de la communauté scientifique de la physique des hautes énergies pensaient qu'on allait découvrir plusieurs particules relevant d'une des versions supersymétriques du modèle standardmodèle standard de cette physique. Futura avait consacré précédemment un long article aux théories supersymétriques, article que l'on peut trouver sous celui-ci.

En outre, on espérait même que certaines de ces particules seraient précisément celles dont on a besoin pour expliquer la nature de la matière noirematière noire gouvernant le monde des galaxiesgalaxies et des amas de galaxiesamas de galaxies. Si le boson BEH a bien été découvert, c'est pour le moment la déception avec les particules de matière noire. Certains pensent même qu'elles n'existent pas et qu'il faut plutôt modifier les lois de la mécanique céleste de Newton.

Les chercheurs ne se découragent pas pour autant et le Cern vient de faire savoir que le bilan de la chasse aux particules supersymétriques menée avec Atlas de 2015 à 2018, lors de la seconde période de production de collisions de protonproton, était disponible. Le LHC avait ensuite été arrêté pour permettre de faire des mises à jour. La troisième campagne de recherche, le Run 3, a, elle, démarré en juillet 2022 à une énergie inédite de 13,6 TeV et avec des faisceaux plus lumineux, donc capables de produire plus rapidement des collisions susceptibles de faire apparaître de nouvelles particules. Certaines réactions sont en effet très peu probables dans une seule collision de deux protons, de sorte que pour avoir une chance de voir une réaction productrice d'une particule exotiqueexotique en quelques années tout au plus, il faut multiplier le nombre de collisions par seconde et donc la luminositéluminosité des faisceaux.

L'analyse des données du Run 2 n'a pas permis de mettre en évidence de nouvelles particules, mais elle a posé de nouvelles contraintes sur les théories de particules supersymétriques possibles - notamment sur les massesmasses que certaines d'entre elles pourraient avoir. Certaines versions des théories supersymétriques ont été exclues et, dans certaines d'entre elles, on sait désormais que ces particules ne peuvent pas avoir environ la moitié des masses des bosons BEH ou Z, et cela grâce à de nouvelles techniques d'analyse dont certaines sont basées sur l'apprentissage machine, le fameux deep learning.

Il y a quelque temps aussi, les membres de la collaboration Atlas ont fait état des résultats de la chasse aux mythiques monopôles magnétiquesmonopôles magnétiques également au cours du Run 2. Ces monopôles doivent se comporter comme des particules chargées également et, en fait, comme si elles étaient nettement plus chargées que de simples électronsélectrons ou protons, ce qui veut dire qu'elles ont un fort pouvoir ionisant en traversant les matériaux et donc les parois du détecteur géant où elles déposeraient beaucoup d'énergie.

Des signatures ont été cherchées pour des particules avec des charges électriques de 20e, 40e, 60e, 80e et 100e, où « e » est la charge électrique élémentaire d'un électron, et en supposant que des monopôles pouvaient avoir des énergies de 0,2 TeV à 4 TeV.

Rien n’a été trouvé, mais là aussi de nouvelles contraintes sur les théories avec ces particules exotiques ont été posées.

De l'antimatière aux monopôles magnétiques de Dirac

La chasse se poursuivant avec le Run 3, c'est une bonne occasion de reprendre les explications que Futura avait déjà données sur la saga des monopôles magnétiques.

Tout le monde peut constater qu'il n'est pas possible de séparer les pôles nord et sud d'un aimant afin d'obtenir des charges magnétiques élémentaires isolées d'un seul signe, alors que c'est le cas pour les électrons ou les protons. Dit autrement, alors que des monopôles électriques de charges opposées existent, il ne semble exister que des dipôles magnétiques.

Or, les équations de Maxwelléquations de Maxwell décrivant le champ électromagnétiquechamp électromagnétique couplé à des charges électriques dans le formalisme adapté à l'existence de l'espace-tempsespace-temps se rassemblent en deux groupes, presque identiques. Cette dualité reflète parfaitement le fait qu'un champ électriquechamp électrique pour un observateur est un champ magnétiquechamp magnétique pour un autre, et inversement. Ces deux groupes d'équations deviennent encore plus symétriques et élégants si l'on introduit en plus des courants de charges électriques dans l'espace-temps des courants de charges magnétiques, donc des monopôles magnétiques.

En se basant sur cette constatation, Paul Dirac est allé plus loin en 1931, peu de temps après avoir découvert, sur le plan théorique, l'existence de l'antimatière. En effet, toujours en cherchant à combiner les lois de la mécanique quantiquemécanique quantique à celles de la relativité, il a découvert que la théorie quantique autorisait l'existence de monopôles magnétiques si le produit de la charge électrique élémentaire et d'une charge magnétique élémentaire était égal à un multiple entier de la constante de Planckconstante de Planck.

Dans ce cadre, des monopôles magnétiques sont possibles et, de plus, ils expliquent l'origine de la quantificationquantification de la charge. Toutefois, la théorie de Dirac restait muette sur la valeur des masses d'un électron, d'un proton ou d'un hypothétique monopôle magnétique.

Des monopôles électrofaibles pendant le Big Bang ?

Le sujet est revenu sur le devant de la scène au cours des années 1970 et au début des années 1980 quand plusieurs chercheurs, dont le prix Nobel de physique Gerard 't Hooft, ont compris que dans les théories unifiant les forces électromagnétiques et nucléaires découvertes ces années-là, des analogues de monopôles de Dirac devaient exister si l'on supposait l'existence de champs de bosons de Brout-Englert-Higgs supplémentaires. La théorie unifiée électrofaible gagnait de plus en plus en crédibilité pendant cette période et elle postulait l'existence d'un champ de bosons BEH.

Mais ces monopoles devaient être fantastiquement lourds, très probablement 10¹⁶ fois plus qu'un proton, donc impossible à produire en accélérateur de particules sur Terre (rappelons que le LHC ne peut produire au mieux dans ces collisions que des particules environ 13 000 fois plus lourdes qu'un proton). Toutefois, les physiciensphysiciens Tom W. B. Kibble puis Wojciech H. Zurek avaient également découvert qu'aux hautes températures du tout début du Big BangBig Bang, les énergies étaient suffisamment élevées pour produire massivement ces monopôles. Très probablement stables, on pouvait espérer en détecter dans le rayonnement cosmique.

Ce ne fut jamais le cas et le développement de la théorie de l'inflation a laissé penser qu'en fait, si ces monopôles avaient été produits, la phase inflationnaire de l'expansion de l'espace devrait avoir tellement dilué le contenu du cosmoscosmos primordial qu'il n'y avait aucune chance d'en détecter.

Toutes ces idées sont à nouveau revenues sur le devant de la scène de façon surprenante, depuis environ 10 ans, quand les physiciens se sont convaincus que contrairement à ce qu'ils pensaient depuis les années 1970, la théorie électrofaiblethéorie électrofaible de Glashow-Salam-Weinberg contenait elle aussi des monopôles magnétiques mais qui devaient posséder des masses beaucoup plus faibles. Et même, si peu élevées que des collisions au LHC pouvaient peut-être en produire, ou pour le moins avec des protons dans le rayonnement cosmique à des énergies certes encore inatteignables avec le LHC mais ne nécessitant pas, et de loin, les énergies du début du Big Bang.

La supersymétrie ne s'est pas encore montrée au LHC

Article de Laurent SaccoLaurent Sacco, publié le 01/03/2011

Existe-t-il un supermonde ? Un monde où les coordonnées de l'espace-temps comprennent d'autres dimensions généralisant la géométrie ordinaire, donnant naissance aux particules de matière noire et expliquant l'énergie noireénergie noire ? Un premier bilan de la recherche d'un tel monde avec le LHC a été publié sur arXivarXiv.

L'un des domaines de recherche les plus actifs en physique des hautes énergies depuis plus de trente ans est sans conteste celui des théories quantiques des champs supersymétriques. La supersymétriesupersymétrie fascine certains par son élégance mathématique et physique ou au contraire en rebute d'autres à cause de la prolifération des paramètres physiques libres qu'elle introduit dans la théorie de champs de particules. Pour le seul modèle standard, 19 paramètres libres ne sont pas fixés par la théorie, par exemple les masses des quarksquarks, de l'électron, du muonmuon et du tauon. Ce nombre augmente si l'on introduit les masses des neutrinosneutrinos révélées par la découverte du phénomène d'oscillation expliquant l'anomalieanomalie des neutrinos solaires.

Si l'on cherche à introduire une généralisation supersymétrique du modèle standard, le nombre de paramètres libres peut dépasser la centaine. Pour certains, il ne s'agirait donc pas d'un progrès dans la compréhension plus profonde du monde des particules, réduisant la complexité des phénomènes à un ensemble de lois plus simples et plus générales. Pire, les nouvelles particules introduites dans le cadre des théories des champs quantiques supersymétriques refusent obstinément de se montrer dans les expériences en accélérateur depuis au moins vingt ans.

Certes, les masses de ces nouvelles particules ne sont pas complètement déterminées par la théorie. On sait juste qu'elles doivent être plus lourdes que les particules du modèle standard. Mais les contorsions des théoriciens repoussant chaque fois plus haut les échelles d'énergies auxquelles ces particules doivent se manifester amènent certains chercheurs à penser qu'il s'agit à chaque fois d'« épicycles » supplémentaires ajoutés à une belle théorie pour la sauver du désastre. Les défenseurs de la supersymétrie seraient donc un peu comme le jeune bâtisseur du ciel Kepler ou les derniers défenseurs du modèle géocentriquegéocentrique de PtoléméePtolémée, s'obstinant à conserver la figure parfaite du cercle pour expliquer les orbitesorbites du Système solaireSystème solaire.

Mais qu'est-ce que la supersymétrie et pourquoi s'est-elle introduite dans les modèles des champs de matière et de forces décrivant le cosmos observable et son évolution du Big Bang au Vivant ? Il n'est pas possible de donner une réponse courte et non technique. 

Une généralisation de l'algèbre et de la géométrie

Dans la longue marche ayant conduit du calcul sur les nombres entiers aux calculs sur les « nombres » supersymétriques, une première étape fut de reconnaître que les nombres réels décrivaient la structure d'une droite et que les opérations sur ces nombres étaient liées à des positions et transformations de points sur une ligne. La seconde étape a été franchie lorsque l'on a découvert les nombres complexes et que des mathématiciensmathématiciens comme Caspar Wessel, Jean-Robert Argand et surtout Carl Friedrich Gauss les relient aux points du plan.

Pendant tout le XIX^e siècle, les mathématiciens vont alors se rendre compte que les fonctions des nombres complexes sont des outils puissants pour résoudre des problèmes de physique ou de géométrie sur une surface. Les transformations géométriques que sont les translationstranslations, les rotations, les dilatationsdilatations et projections et qui sont à la racine de bien des théorèmesthéorèmes de géométrie dans le plan sont elles aussi bien capturées par l'algèbre des nombres complexes.

Pendant ce même siècle, des mathématiciens comprennent que si l'on peut associer au point d'un plan de nouveaux nombres, il doit en être de même des points de l'espace et c'est ainsi que Hamilton fit la découverte des quaternions et que se développera l'algèbre des nombres hypercomplexes.

L'avant-dernière étape pour la supersymétrie est la découverte de l'espace-temps. Naturellement, l'équivalent des nombres hypercomplexes pour l'espace-temps est rapidement découvert. Ce sont les spineurs.

Enfin, c'est vers le début des années 1970 que plusieurs chercheurs, comme Julius Wess et Peter van Nieuwenhuizen, approfondissant le rôle de ces spineurs dans les théories quantiques des champs relativistes, découvrent des généralisations des opérations de symétrie que sont les translations et les rotations dans l'espace-temps.

Les théories supersymétriques voient le jour...

Les particules du modèle standard et leurs partenaires supersymétriques. © ENS

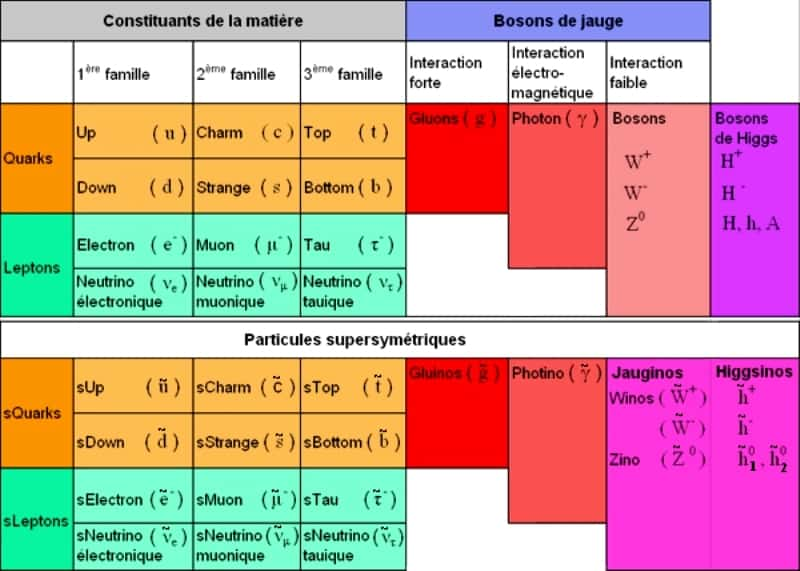
Une théorie miraculeuse mais multipliant les particules

Avec stupéfaction, et d'année en année, les théoriciens découvrent les propriétés miraculeuses de ces théories. Ainsi, elles permettent d'éliminer dans certains cas les problèmes de divergences infinies apparaissant en théorie quantique des champs, rendent possibles l'unification des forces nucléaires fortes avec l'interaction électrofaible à hautes énergies et introduisent naturellement une particule de matière noire, le neutralinoneutralino (ayant les bonnes propriétés demandées pour expliquer les observations en cosmologiecosmologie). Plus incroyable encore, la supersymétrie permet de déduire les équations de la relativité généralerelativité générale d'EinsteinEinstein, incluses dans une généralisation de cette dernière, la supergravitésupergravité.

Pour cela, la théorie demande qu'à chaque particule du modèle standard, que ce soit un fermionfermion (une particule de matière comme un quark) ou bien un boson (vecteur des interactions, comme un gluongluon), soit associé son partenaire supersymétrique. Le partenaire d'un fermion doit être un boson et inversement. Cette idée ouvre ainsi la voie vers une unification vertigineuse entre particules de matière et particules médiatrices des interactions. Mais pour que ces nouvelles particules aient jusqu'ici échappé à toute détection en accélérateur, elles doivent être beaucoup plus lourdes que leur partenaire du modèle standard.

On a pris l'habitude de nomme des partenaires supersymétriques en ajoutant la lettre s au début du nom ou un os à la fin. Le bestiaire des particules s'enrichit ainsi des squarkssquarks, des sleptons, comme le sélectron, ou encore des gluinos, photinosphotinos et Higgsinos. Mais malheureusement aussi, le nombre de paramètres libres augmente en même temps...

On retrouve en outre un vieux problème, celui de la constante cosmologiqueconstante cosmologique, considéré comme la pire prédiction de la physique théorique et qui est en lien avec l'énergie noire.

MSSM et mSUGRA

Ces particules supersymétriques ont été cherchées avec le LEP et le Tevatron. Il est possible de réduire le nombre de paramètres libres en imposant des contraintes ou des hypothèses simplificatrices. Bien que les masses des particules ne soient toujours pas univoquement déterminées, il émerge en effet des prédictions concernant, par exemple, la bande d'énergie où doit se trouver la masse du boson de Higgsboson de Higgs (en dessous de 130 fois la masse du proton environ) dans le cas de ce qu'on appelle le modèle standard supersymétrique minimal (MSSM).

Certaines réactions entre particules du modèle standard à hautes énergies produisent des neutralinos très difficiles à détecter directement mais qui se trahissent par des déficits d'énergie dans les bilans des réactions dans des détecteurs comme CMS ou Atlas. Les grandes structures de l'universunivers observable posent elles aussi des contraintes sur les particules supersymétriques... pourvu qu'elles constituent bien une part importante de la matière noire ! Généralement, la grosse centaine de paramètres libres se réduit à seulement 5 si l'on connecte le MSSM à un modèle minimal de supergravité que l'on appelle mSUGRA.

Comme on l'a déjà dit, la supersymétrie a ses défenseurs et ses détracteurs, ou tout simplement des chercheurs qui sont quelque peu sceptiques. Tout le monde attend donc impatiemment les résultats des collisions au LHC et ce que donnent les analyses des données enregistrées par Atlas et CMS.

Déjà en 2008 on pouvait constater la diversité des opinions des prix Nobel de physique au sujet de ce que verrait le LHC et l'on parlait même déjà d'un calendrier possible pour la découverte du boson de Higgs.

Des recherches seulement préliminaires

En début d'année 2011, les chercheurs de CMS puis d'Atlas ont publié les premiers résultats concernant la chasse aux particules supersymétriques au LHC. Des paires de squarks et de gluinos sont les superparticules les plus faciles à produire au LHC. Chaque paire de squark-gluinos donne dans le cas des modèles de supersymétrie les plus étudiés des jets de quarks avec de l'énergie manquante emportée par les neutralinos indétectables. Sous certaines hypothèses sur les masses des squarks et des gluinos, les chercheurs ont été capables d'établir de nouvelles bornes pour la supersymétrie. Ainsi les masses de ces deux particules, dans les modèles simples étudiés, doivent maintenant être supérieures à 700 GeV environ. Si cela n'était pas le cas, on aurait vu les jets de quarks avec les déficits d'énergie, causés par la production des particules supersymétriques aux énergies actuellement accessibles dans les collisions au LHC.

L'espace des paramètres libres possibles pour les modèles simples avec mSUGRA est devenu encore plus restreint mais comme il s'agit de toute façon d'une idéalisation approximative de la réalité, sous réserve qu'elle soit supersymétrique, on peut dire que pour le moment il n'existe toujours pas de raisons sérieuses d'abandonner les recherches  concernant la pertinence de la supersymétrie pour décrire l'univers observable, en particulier la matière noire.

Nous n'en sommes encore qu'au début de l'exploration possible avec le LHC en ce qui concerne la supersymétrie.

Les publications sur arXiv concernant les recherches réalisées avec Atlas et CMS ont été commentées sur plusieurs blogsblogs, en particulier celui de Adam Falkowski et Tommaso Dorigo. Un article cosigné par John Ellis (voir les liens en bas de cet article) étudie aussi les implications des recherches effectuées au LHC sur la supersymétrie.