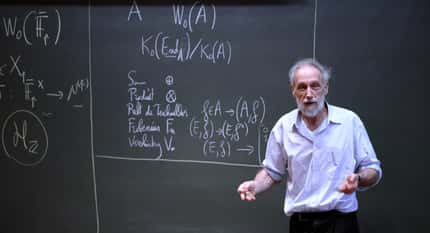au sommaire

Peter Higgs a été le premier à parler explicitement d'un boson associé au mécanisme qu'il a découvert avec d'autres physiciens, capable d'expliquer la masse des particules élémentaires du modèle standard. © Peter Tuffy, The University of Edinburgh
Depuis des années, le brillant mathématicienmathématicien français lauréat de la médaille Fields de mathématique, Alain Connes, développait une théorie unifiée des forces de l'univers, capable non seulement de combiner les équations de la relativité générale d'EinsteinEinstein avec celle du modèle standard des particules élémentaires, mais aussi d'expliquer l'origine du boson de Higgsboson de Higgs. Il s'agissait d'une nouvelle version des théories de Kaluza-Klein faisant dériver la nature des forces du cosmoscosmos de la géométrie d'un espace-tempsespace-temps de dimension supérieure à 4. Mais alors que dans les théories de Kaluza-Klein classiques, sous-jacentes à la théorie des supercordesthéorie des supercordes, les dimensions supplémentaires de l'espace sont sous forme d'objets géométriques continus (comme une sphère ou des tores en 7 dimensions), la théorie d'Alain Connes fait intervenir des espaces discrets.
Remarquablement, en introduisant deux espaces-temps constituant deux feuillets séparés par une distance non nulle, mais sans que de l'espace existe entre les deux, le champ de Higgs avec le mécanisme de Brout-Englert-Higgs donnant la massemasse des particules élémentaires du modèle standard, émergeait naturellement des équations, sans avoir besoin de postuler sa présence.
Un modèle standard non commutatif
Le tour de force de la théorie d'Alain Connes est sa capacité à engendrer les équations de la relativité générale couplées aux équations de Yang-Mills du modèle standard avec leurs groupes de Lie. Cette capacité repose de façon fondamentale non pas tant sur une nouvelle formulation des théories de Kaluza-Klein mais sur l'hypothèse que la géométrie de l'espace-temps n'est pas décrite par la géométrie courbe à n dimensions classiques de Riemann, mais sur une nouvelle géométrie : la géométrie non commutative.

Le mathématicien Alain Connes doit avoir retrouvé le sourire. Sa théorie unifiée des interactions est de retour dans le monde de la physique théorique car elle est finalement compatible avec un boson de Higgs léger. © Renate Schmid-Wikipedia
En partie inspirée par les travaux de Von Neumann sur les équations de la mécanique quantiquemécanique quantique mise au jour par Heisenberg, Born et Jordan vers 1925, cette géométrie non commutative a été découverte et développée par Alain Connes lui-même. Elle est malheureusement assez complexe à saisir et plusieurs physiciensphysiciens travaillant dans le domaine des particules élémentaires avouent humblement ne pas vraiment la comprendre. Elle représente en tout cas une alternative intéressante et crédible à la théorie unifiée des interactions la plus prometteuse depuis 30 ans, la théorie des supercordes.
Un boson de Higgs léger à partir d'un autre champ scalaire
Or, la théorie d'Alain Connes semblait prédire une masse pour un boson de Higgs standard de 170 GeVGeV de façon très rigide. Il en résultait que l'exclusion de cette masse par les chercheurs du Tevatron avec une publication retentissante en août 2008 signait l'arrêt de mort de sa théorie, au moins dans sa forme primitive. Il fallait en effet être prudent. Les théories de Yang Mills à la base du modèle standard semblaient elles aussi réfutées par l'expérience avant que l'on ne découvre le mécanisme de Brout-Englert-Higgs et le boson de Higgs associé.
De fait, en août 2012, comme il l'indique sur un blogblog dédié à la géométrie non commutative, Alain Connes déposait sur arxiv avec son collègue et collaborateur de longue date, Ali Chamseddine, un nouvel article révolutionnaire. En examinant de nouveau le contenu en particules de sa théorie, Alain Connes a réalisé qu'il avait eu tort de négliger la présence potentielle d'un nouveau champ inclus dans les équations et pouvant se combiner à celui du boson de Higgs.
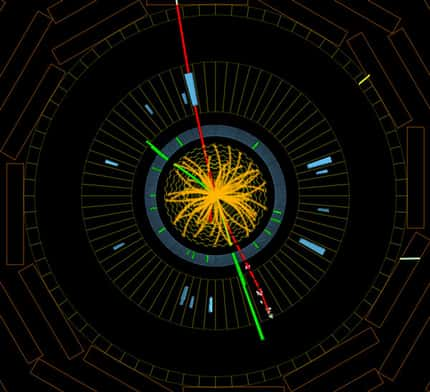
De façon spectaculaire, la prise en compte correcte de ce champ, sans postuler un nouvel élément étranger à sa théorie de départ, permet de faire baisser la masse du boson de Higgs. Elle est désormais compatible avec les 126 GeV du boson récemment découvert au LHCLHC et qui semble bel et bien être celui de Peter HiggsPeter Higgs. Le modèle standard non commutatif d'Alain Connes incluant la relativité générale d'Einstein vient donc de ressusciter !
Détrônera-t-il la théorie des supercordes ? Difficile à dire pour le moment, d'autant plus que la théorie des cordesthéorie des cordes semble prédire elle aussi une géométrie non commutative pour l'espace-temps. Les deux théories sont peut-être complémentaires.
Les lecteurs souhaitant en savoir plus et qui possèdent le bagage minimum nécessaire pourront consulter ces deux références :