Méthode des vitesses radiales : qu'est-ce que c'est ?

La méthode des vitesses radiales est l'une des principales méthodes utilisées en exobiologie et en astronomie pour détecter des exoplanètes. On s'en sert souvent au sol pour vérifier et compléter une découverte d'exoplanète faite dans l'espace par des satellites comme Kepler et CorotCorot qui eux utilisent la méthode du transit planétaire.

Principe de la méthode des vitesses radiales

Pour comprendre le principe de la méthode des vitesses radiales, prenons le cas le plus simple. Considérons donc un système formé d'une seule planète en orbite circulaire autour de son étoileétoile et vue par un observateur dans le plan de son orbite. C'est-à-dire que l'angle i que fait la normale au plan de l'orbite avec la ligne de visée vaut 90°. Les lois de la mécanique céleste impliquent que l'attraction gravitationnelle de la planète sur l'étoile lui impose un mouvementmouvement de révolution autour du barycentrebarycentre du système, le plus souvent à l'intérieur de l'étoile.

Le principe de la détection d'une exoplanète par la mesure d'un décalage spectral par effet Doppler-Fiezeau. © ESO

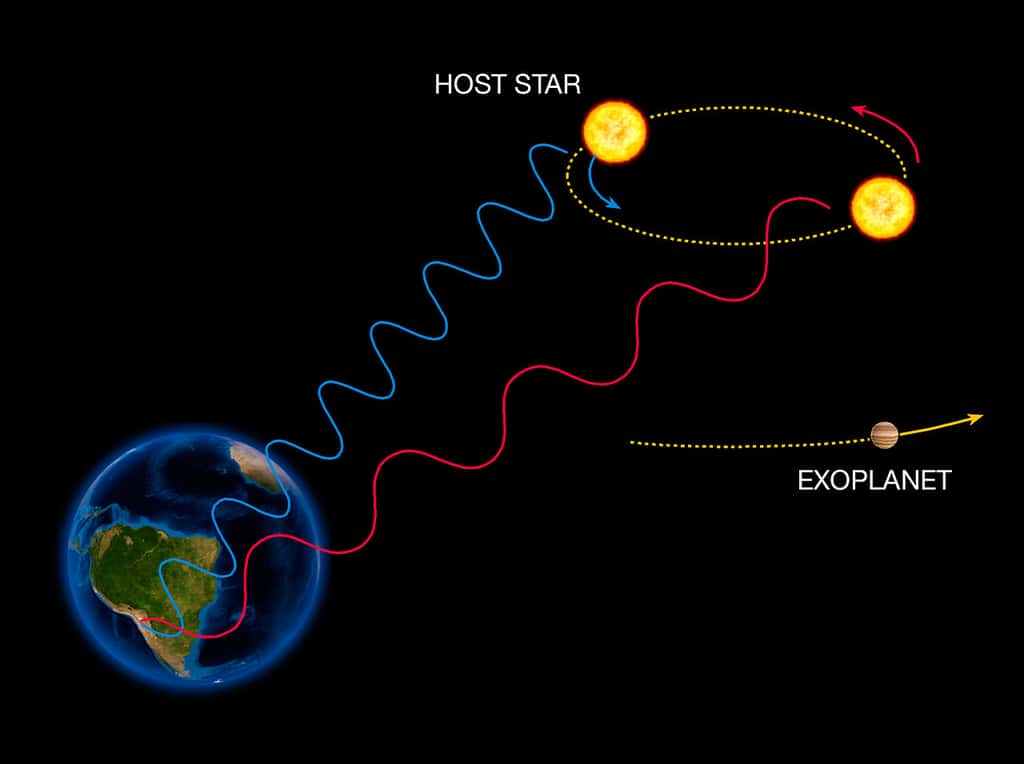
L'étoile va donc s'approcher puis s'éloigner de l'observateur avec une composante de vitesse radiale qui varie périodiquement. La lumièrelumière de l'étoile va alors subir un effet Doppler-Fizeaueffet Doppler-Fizeau se traduisant par un décalage spectral passant périodiquement du bleu au rouge (voir le schéma ci-dessus).

Mesure de vitesse radiale V_r en m/s de l'étoile 51Peg en fonction du temps en abscisse (jours). L'inclinaison i est inconnue, donnant une masse au moins égale à 0,45 fois la masse de Jupiter pour l'exoplanète. © Butler et Marcy, media4.obspm.fr, Fenêtres sur l'Univers

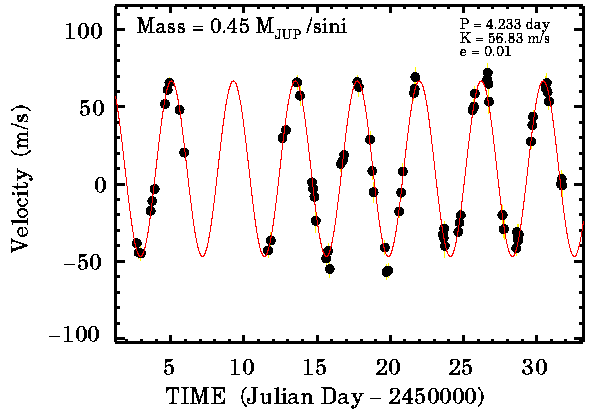
Si l'on dispose d'un spectroscope avec un pouvoir de résolutionrésolution suffisant, on peut mesurer ce décalage et en déduire une valeur de vitesse radiale. La courbe de variation de la vitesse radiale fournit alors une période TT et une amplitude donnant la composante parallèle V_r à la ligne de visée de la vitesse de l'étoile. La théorie de l'évolutionthéorie de l'évolution stellaire permet, quant à elle, de déduire du spectrespectre de l'étoile sa massemasse M.

L'excentricité de l'orbite elliptique de l'étoile HR 108147, voisine de 0,5, et la géométrie de l'observation conduisent à une telle courbe de vitesse radiale plus complexe que dans le cas le plus simple avec une orbite circulaire. Le schéma du dessous représente les résidus entre les valeurs observées et la courbe de vitesse modélisée. © Observatoire de Genève, media4.obspm.fr, Fenêtres sur l'Univers

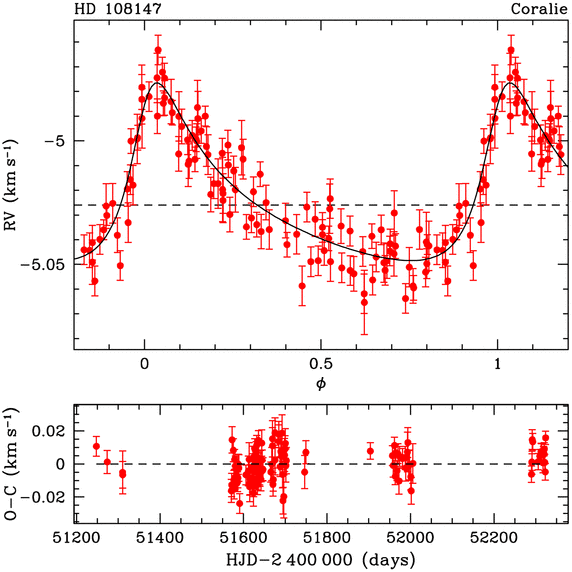
De ces trois grandeurs M, V_r et T, il est possible d'en déduire la distance de la planète à son étoile et sa masse m. En général, la valeur de l'inclinaison i de la normale au plan de l'orbite par rapport à la ligne de visée n'est pas connue. On mesure seulement la grandeur m sin(i) et donc une borne inférieure pour la masse réelle de la planète.

La courbe de vitesse radiale de l'étoile HD 168443 présente deux composantes, dues à deux compagnons planétaires. Les orbites des deux planètes détectées autour de HD 168443 ont des périodes d'ordres de grandeur bien distincts et une excentricité élevée (0,53 et 0,23). © Butler et Marcy, media4.obspm.fr, Fenêtres sur l'Univers

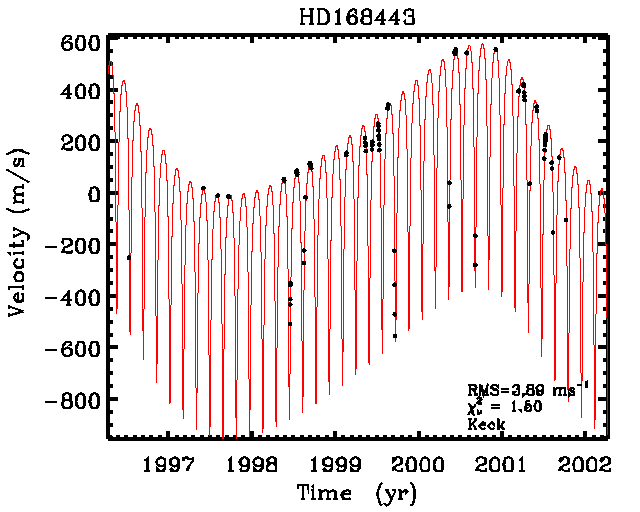
D'autres complications surgissent. L'orbite peut ne pas être circulaire mais elliptique et il peut y avoir plusieurs exoplanètes en orbite. La courbe de variation de la vitesse radiale est alors plus compliquée mais elle est aussi plus riche en informations utilisables. Ce n'est plus une simple sinusoïde mais on peut quand même en déduire les périodes et les excentricitésexcentricités des orbites des exoplanètes, ainsi que des estimations de leurs masses.

La courbe de vitesse pour l'étoile HR 82943 montre deux exoplanètes avec des orbites non circulaires. © Observatoire de Genève, media4.obspm.fr, Fenêtres sur l'Univers

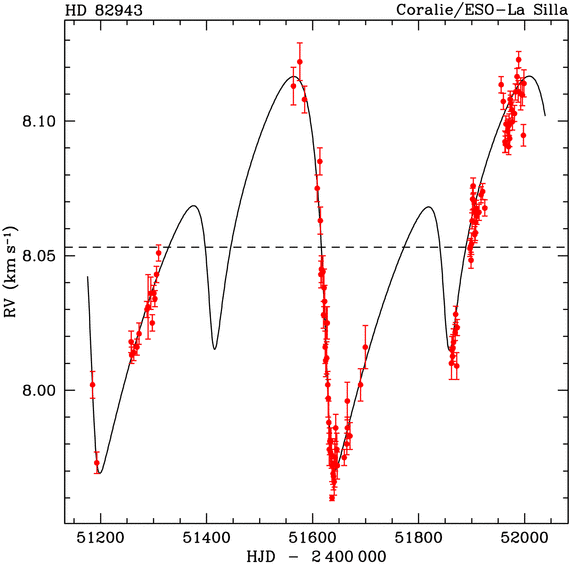
En pratique, la méthode des vitesses radiales ne permet de détecter facilement que des planètes géantes orbitant à une distance proche de leurs étoiles. Dans ce cas, la perturbation gravitationnelle est forte et le mouvement de l'étoile est important. C'est pourquoi ce sont des Jupiter chaudes qui ont été détectées en premier, comme ce fut le cas de Pegasi 51b en 1995 par Michel Mayor et Didier Queloz.

Il est particulièrement difficile de détecter des exoterresexoterres, surtout si elles sont en orbite autour d'une étoile de type solaire et à une distance les plaçant dans la zone d'habitabilitézone d'habitabilité. Pour cela, il est plus efficace d'utiliser la méthode du transit planétaire.