au sommaire

Le physicien théoricien Eugène Wigner est célèbre pour son analyse du rôle des symétries et de la théorie des groupes en mécanique quantique. Comme Schrödinger, il s'intéressait au mysticisme du Vedanta indien. © BME OMIKK, 2005
L'une des hypothèses fondamentales sur lesquelles Werner HeisenbergWerner Heisenberg s'est appuyé en 1925 pour découvrir les premiers éléments de la formulation matricielle de la mécanique quantique est celle du rejet de la notion de trajectoire d'une particule. Dans les articles suivants, il développe une théorie quantique générale de la mécanique analytique d'un système physique dans l'espace des phases en compagnie de Max BornMax Born et Pascual Jordan. Ce rejet d'une trajectoire pour les coordonnées spatiales d'un tel système y est toujours présent, sous une forme généralisée.
En 1926, l'autre formulation de la quantificationquantification de la mécanique analytique classique, à savoir la mécanique ondulatoire de Schrödinger, va faire apparaître la fameuse fonction d'onde d'un système mécanique. Max Born va découvrir qu'élevée au carré, elle donne la densité de probabilité d'état de ce système dans une région de l'espace des phases pour ses coordonnées de position. Parallèlement, l'équivalent de la fonction d'onde de Schrödinger est introduit pour des valeurs des impulsions d'un système mécanique dans l'espace des phases.
Il ne semblait alors pas évident d'obtenir l'équivalent d'une trajectoire dans cet espace en mécanique quantique, étant donné la perte d'une définition précise simultanée des positions et impulsions impliquée par les inégalités de Heisenberg.

Werner Heisenberg (à gauche) et Eugène Wigner (à droite). Ces deux grands maîtres de la mécanique quantique étaient fascinés par l'importance des symétries mathématiques à la base des particules élémentaires. Heisenberg était influencé par la philosophie de Platon quand il a découvert la mécanique matricielle. © Friedrich Hund
Une connexion avec la formulation classique
En 1932, le grand théoricien hongrois Eugène Wigner, qui fut l'un des premiers à saisir l'importance en mécanique quantique de la théorie des groupes fondée par Galois, découvre qu'il est possible de reformuler la mécanique quantique d'un système physique dans l'espace des phases. On le peut via l'analogue de la fonction de distribution de probabilité classique d'un système mécanique en mécanique statistique. Une telle distribution a été donnée notamment par Josiah Willard Gibbs.
De cette façon, une connexion plus étroite avec la formulation classique, hamiltonienne, d'un système mécanique apparaissait. Comme devaient le montrer plus tard José Moyal et quelques autres à partir des travaux de Wigner et du grand mathématicienmathématicien Hermann WeylHermann Weyl, il devenait possible de préciser comment obtenir la formulation quantique des équations d'un système physique classique.
L'un des avantages de la formulation de la mécanique quantique à partir de la fonction de Wigner (qui donne donc la probabilité d'avoir des valeurs données des coordonnées de position et d'impulsion d'un système lors d'une mesure) est de fournir une connexion avec la notion de flot classique dans l'espace des phases d'un système dynamique.
Dans cette vidéo, les portraits de phase d'équations différentielles avec des attracteurs étranges « dansent » selon les différentes valeurs de certains paramètres influencés par la musique de Johann Sebastian Bach (Klavierkonzert d-moll ─ 3. Allegro). Elle illustre de façon frappante l'ordre complexe régnant derrière certains phénomènes qui semblent purement chaotiques. © Timothy Jones
Une classification topologique des systèmes dynamiques quantiques
On sait que l'on peut faire le portrait de phase d'un système en mécanique classique. C'est-à-dire que l'on peut tracer dans un plan défini avec les coordonnées de position q et d'impulsion p les courbes d'évolution de ce système en fonction de différentes conditions initiales. Ces courbes ressemblent aux lignes de courants d'un fluide et permettent de visualiser d'un coup d'œilœil les différents comportements d'un système mécanique. Henri Poincaré a utilisé de tels portraits de phase pour étudier le problème à N corps en mécanique céleste. Ces portraits permettent aussi de découvrir des attracteurs étranges en théorie du chaos, comme celui de Lorenz.
On peut aussi classifier différents écoulements dans l'espace des phases à l'aide de la topologie. En clair, ces écoulements ne peuvent être déformés continument l'un dans l'autre, de la même façon qu'il n'est pas possible de transformer une sphère en tore en la déformant sans faire de trou dans sa surface. La topologie permet en plus de définir des quantités invariantes, des lois de conservation, avec les flots dans les portraits de phases en physique classique et de révéler finalement des structures ordonnées là où une analyse superficielle ne fait apparaître que du chaos.
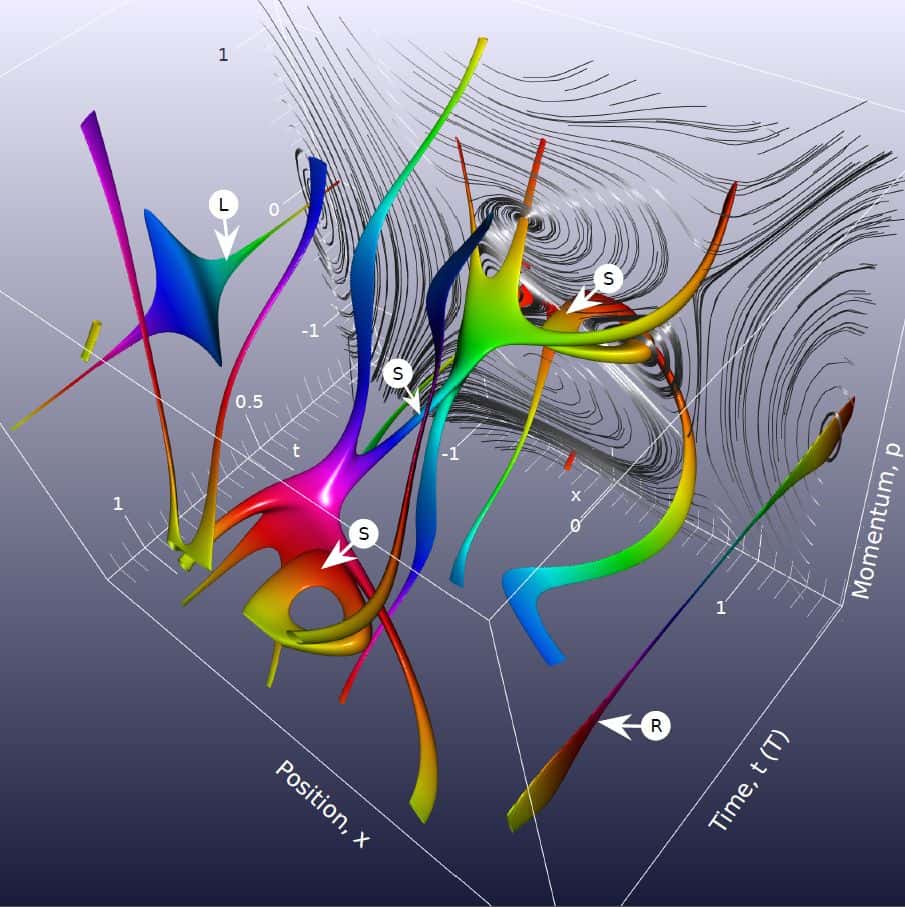
Le portrait de phase étudié avec un flot quantique par des physiciens britanniques est bien visible en arrière-plan à droite sur cette image. Son évolution dans le temps s’effectue selon les trajectoires colorées de certains centres de « tourbillons », et est dictée par des lois de conservation analogues à celle de la charge électrique, mais ici d'origine topologique. Pour plus de détails, se reporter à l'article des Physical Review Letters. © Université du Hertforshire
Dans un article récemment publié dans les célèbres Physical Review Letters, des physiciensphysiciens de l'université du Hertfordshire (Royaume-Uni) viennent de montrer qu'il était aussi possible de trouver de telles structures ordonnées dans le flot d'un système quantique. Ils s'appuient sur le fait que l'on peut définir l'analogue d'un flot dans l'espace des phases pour un système quantique, malgré l'impossibilité de définir une trajectoire précise en mécanique quantique comme l'avait découvert Heisenberg (du moins dans la formulation qui n'est pas celle de David Bohm). Tout comme en mécanique hamiltonienne classique, il apparaît alors des sortes de tourbillonstourbillons dans les flots de l'espace des phases, mais avec des caractéristiques qui sont propres à la mécanique quantique. De nouvelles lois de conservation topologique ont ainsi été découvertes par les chercheurs.
Selon eux, elles permettent de découvrir de nouveaux aspects de l'effet tunnel en mécanique quantique, découvert en physique quantiquephysique quantique par Georges GamowGeorges Gamow. Rappelons qu'il s'agit d'un effet qui rend possible le fait que le SoleilSoleil brille et qui intervient à la racine de bien des phénomènes de liaison chimiqueliaison chimique, en physique du solidesolide pour l'électronique et même dans certains modèles de cosmologie quantique.