au sommaire

Une initiation à la géométrie, ludique et accessible. © DR
La géométrie est une partie des mathématiques, qui étudie les figures composées de lignes, de points, de surfaces. Elle permet d'appréhender les notions d'espace. Parfois pointue, elle peut être abordée de façon simple, comme dans ce dossier.
Les fondateurs de la géométrie et les mathématiciens grecs
Les mathématiciensmathématiciens grecs les plus célèbres sont probablement Pythagore et EuclideEuclide, mais le véritable père de la géométrie est ThalèsThalès.
Au cœur de la géométrie : les invariants et la symétrie
Quand les gens parlent de symétrie, ils évoquent généralement la vision d'images dont l'ensemble est agréablement équilibré, comme la symétrie des ailes de papillon, le dessin des pépins quand vous coupez une pomme en deux, ou un visage vu de face.
Qu'est-ce qu'un objet mathématique, vous demandez-vous ? Un objet mathématique se distingue d'un objet réel en ce qu'il est idéal, c'est-à-dire parfait.
Quand on s'aperçut que la Terre n'était pas plate mais sphérique, de nombreux « faits » de la géométrie euclidienne qui semblaient évidents devinrent problématiques et ouvrirent la voie aux géométries non euclidiennes.
Pi : le rapport de la circonférence au diamètre
Il y a bien longtemps les géomètresgéomètres comprirent que la longueur de la circonférence d'un cercle valait environ trois fois son diamètre. Dans le papyrus Rhind, PiPi était égal au carré de 16/9, soit 3,16049. Les Babyloniens avaient calculé que le rapport était légèrement supérieur à 3 et utilisaient 3 1/8, très proche de l'approximation que l'on donne dans les livres d'école, 3 1/7. Au IIIe siècle de notre ère, le mathématicien chinois Liu Hui inscrivit un polygone de 292 côtés dans un cercle, puis un autre polygone de 3.072 côtés pour calculer Pi. Il trouva 3,141024.
La géométrie des nombres : nombres naturels et fractions
Bien que son théorème soit de nature géométrique, la plus grande gloire de Pythagore repose sur ses découvertes en théorie des nombres. Un problème lancinant était le calcul de la longueur de la diagonale d'un carré de côté unité. Les Babyloniens avaient calculé cette longueur avec six décimales, mais les Pythagoriciens savaient que ce n'était qu'une approximation. Quelle était la valeur exacte ? Pythagore montra que ce ne pouvait être une fraction.
La géométrie projective pour représenter la perspective
Principe bien connu des dessinateurs, la représentation de la perspective doit être maîtrisée pour être parfaitement réussie. C'est ce à quoi s'emploie la géométrie projective, l'étude des projections des objets sur un plan.
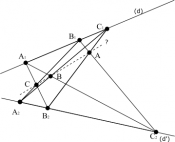
Au cœur de la géométrie projective se trouve le théorème de Pappus. Voyons ici ses applications.
Découvrir et acheter le livre de l'auteur sur la géométrie
Pour aller plus loin sur le sujet de la géométrie, découvrez aux Editions Belin le livre consacré à cette science mathématique.