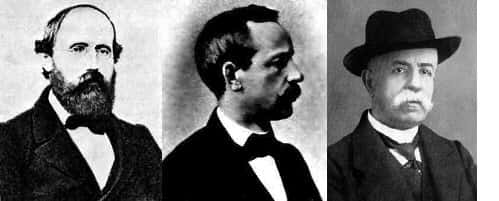Les singularités en relativité générale et le cylindre de Tipler

Voyons ici les singularités en relativité générale et le cylindre de Tipler.

 
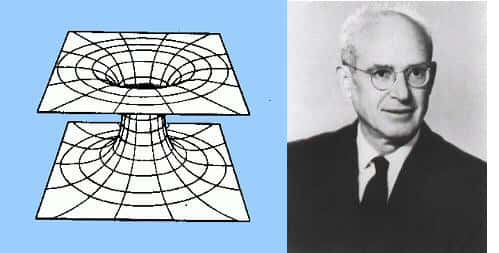
Roger Penrose. © University of Georgia / Stephen Hawking. © Nasa

Singularités et relativité générale

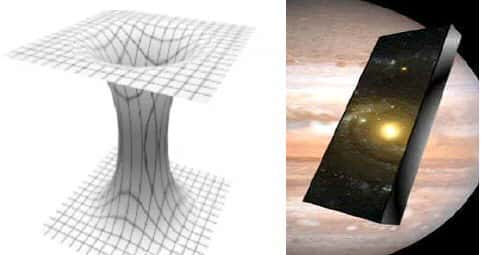
L'existence d'une singularité au cœur de la solution de Schwarzschild ne permet pas, on l'a vu, de traverser le pont d'EinsteinEinstein Rosen associé sans se faire complètement écraser. Une question vient alors naturellement, la solution est quand même très particulière, symétrie sphérique, un seul paramètre (la masse), ne peut-on espérer trouver une solution plus générale décrivant un espace-temps sans singularité et avec un passage traversable ?

Cette question pose en fait le problème de l'apparition de singularité en relativité générale. Question abordée au milieu des années 1960 par Stephen Hawking, Roger Penrose, Robert Geroch et Georges Ellis dans le cadre de l'effondrementeffondrement des étoiles ou de son analogue, par renversement du temps, dans celui des solutions cosmologiques décrivant des univers en expansion.

En général c'est un problème très compliqué. Si l'on prend le cas d'une étoile, elle n'est pas parfaitement homogène ni sphérique, elle tourne, elle possède un champ magnétiquechamp magnétique et des phénomènes hautement non linéaires se produisent dans la phase finale de l'effondrement de celle-ci, turbulencesturbulences, ondes de choc, réactions nucléairesréactions nucléaires complexes entre les hadronshadrons, etc.

Ils réussirent pourtant, au moyen de méthodes puissantes de la topologie différentielle et de certaines hypothèses physiquesphysiques simples, à prouver que l'apparition de singularité était inévitable.

Penrose, Carter et Hawking s'appuyèrent ainsi sur les diagrammes d'espace-tempsdiagrammes d'espace-temps en traduisant la physique du collapse gravitationnel, les propriétés des trous noirs et l'apparition de singularités, dans des propriétés de topologie et de géométries différentielles associées au comportement de congruences de trajectoires de particules de matièrematière, ou mieux de photonsphotons, en espaces-temps courbes.

On est naturellement conduit à des théorèmesthéorèmes ressemblant à ceux portant sur les lignes de courant en hydrodynamique, ou mieux encore, en optique géométrique.

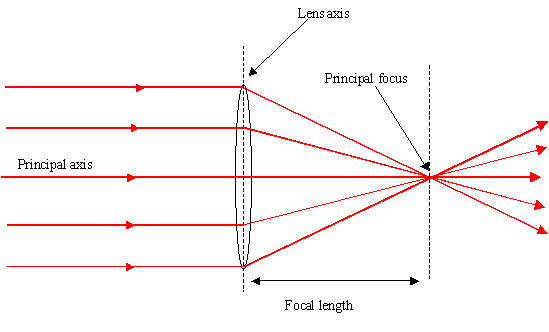
On peut considérer l'horizon un peu comme le bord d'une lentille convergente. © Antonine Education Website

La formation de singularité est alors similaire à l'existence d'un point de convergence des rayons lumineux pour les systèmes optiques. Si l'on considère que l'horizon est un peu comme le bord d'une lentillelentille convergente (cf. le schéma ci-dessus) alors tout ce qui le traverse doit se trouver focaliser en un seul point, le foyerfoyer, qui correspond ici à la singularité centrale.

De la même façon que l'on parle du taux de dilatationdilatation/convergence/rotation des lignes de courant dans un fluide, on aura l'équivalent pour les familles de trajectoires de photons.

Démontrer l'existence d'une singularité sera ainsi lié à l'existence d'un taux de contraction sans limites d'un faisceau de ces trajectoires au fur et à mesure qu'il se déplace sous l'horizon et tel que toutes les trajectoires se focalisent et se terminent en un seul et même point, la singularité.

C'est ce qu'on peut voir sur le schéma ci-dessous :

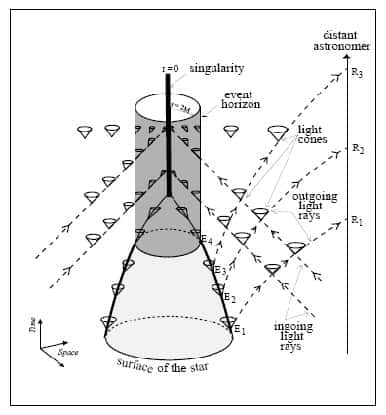
Extrait de Jean-Pierre Luminet -Black Holes: A General Introduction. Voir les explications plus bas. © Jean-Pierre Luminet

Un élément clé des théorèmes est celui de surfaces piégées (trapped surfaces). Tout faisceau lumineux issu de celles-ci verra alors son aire décroître.

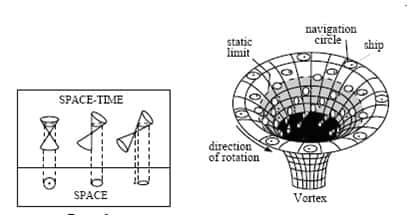
Extrait de de JP Luminet - Black Holes: A General Introduction. Les détails ci-dessous. © Jean-Pierre Luminet

Sur ces trois diagrammes correspondant à la formation d'un trou noirtrou noir par effondrement d'une étoile, ainsi qu'à la structure d'un trou noir de Kerrtrou noir de Kerr en rotation, on voit bien le basculement des cônescônes de lumièrelumière. Remarquez aussi la projection du sommet de la section de cône futur d'un événement donné ainsi que celle de cet événement sous forme de point.

Le caractère inévitable de l'effondrement peut ainsi clairement se voir à partir du comportement du champ des cônes de lumière car ceux-ci s'inclinent au fur et à mesure que l'on se rapproche de l'horizon, sont tangents à celui-ci puis basculent complètement de façon à ce que toutes les trajectoires convergent vers une singularité centrale où l'espace-temps s'anéantit. Rien ne peut donc sortir d'un trou noir et tout ce qui y rentre doit finir par atteindre la singularité très précisément à cause de ce changement de la structure causale de l'espace-temps que les modifications du champ de cônes en champ gravitationnel fort expriment.

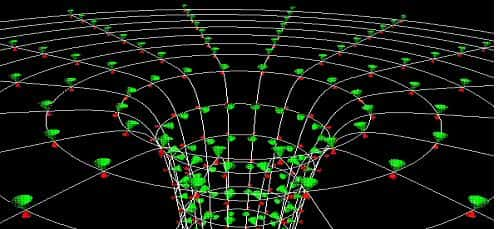
Effondrement de l'espace-temps. © DR

Il faut bien voir, en outre, qu'il arrive un moment où l'ajout d'une pressionpression pour s'opposer à l'effondrement correspond à augmenter tellement la densité d'énergieénergie qu'au lieu de s'opposer à celui-ci, celle-ci le favorise, et c'est l'espace-temps lui-même qui s'effondre.

On ne peut dès lors plus faire intervenir une éventuelle force de répulsion issue de la dégénérescence quantique de composés supposés, mais inconnus, des particules dites actuellement « élémentaires ».

On rappelle en effet que les naines blanchesnaines blanches tirent leur stabilité de la pression de dégénérescencepression de dégénérescence des électronsélectrons, ce qui donne une taille de l'ordre de celle la Terre pour une étoile de la masse du SoleilSoleil. Alors que pour des étoiles à neutrons, beaucoup plus petites car d'un diamètre de l'ordre de quelques dizaines de km seulement, c'est l'interaction nucléaire forte des neutronsneutrons, qui est répulsive à courtes distances, qui entre en jeu.

Pour finir, on retiendra que les théorèmes de singularité reposent sur les deux grandes classes d'hypothèses suivantes.

• Conditions sur l'espace-temps

Surface de Cauchy, pas de boucles temporelles, limites sur la rotation de l'Univers ou des corps.

• Contraintes sur l'énergie 

Conditions fortes, faibles et dominantes sur la positivité de l'énergie. Ce sont ces dernières conditions que Thorne sera conduit à violer pour obtenir des wormholes, elles portent essentiellement sur le tenseurtenseur impulsion-énergie, source du champ de gravitationgravitation.

De manière similaire, l'apparition de singularités en cosmologiecosmologie s'étudiera et s'établira à partir du comportement de basculement des cônes de lumière et de « focalisation » des trajectoires des rayons lumineux au fur et à mesure que l'on remonte dans le temps. C'est ce que l'on voit sur le diagramme suivant :

Extrait de Cern yellow report 91-06 © Ruth M. Williams

Une série de théorèmes importants et très généraux, pour ce qui est de la cosmologie, sont ainsi obtenus conjointement par Hawking et Penrose en 1970. Ce dernier avait donné un premier théorème pour l'effondrement des étoiles en 1965.

En résumé, il n'existerait donc pas de passage à travers l'espace-temps ouvrant à l'humanité la route des étoiles ou la possibilité de voyager dans le temps.

Bye bye 2001 l'odyssée de l'espace ou Les aventures de Valérian et Laureline !

L'odyssée de l'espace et Les aventures de Valérian et Laureline. © DR

Le cylindre de Tipler

La décennie 70 s'achevait alors par le triomphe de la théorie des trous noirs et l'impossibilité d'utiliser ceux-ci comme machines spatio-temporelles.

Et pourtant, quelques signes avant coureurs surgirent simultanément :

Sur ce diagramme on voit bien, à nouveau, le basculement des cônes au fur et à mesure qu'on se rapproche du cylindre et l'apparition de trajectoires possibles vers le passé.

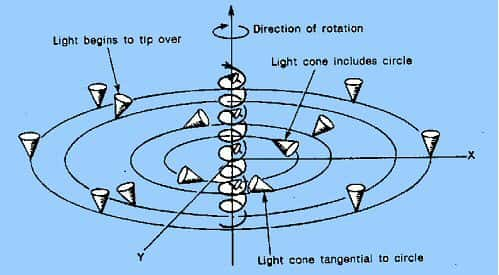
Basculement des cônes.

Plus tard il fut démontré qu'un cylindre de quelques milliers de km de long et possédant la masse et la densité de quelques étoiles à neutronsétoiles à neutrons serait suffisant.

Il est important de bien voir qu'une telle machine ne permet pas de remonter dans le passé plus tôt que la date de sa propre création, ou d'aller plus loin dans le futur que sa date de destruction ou d'arrêt.

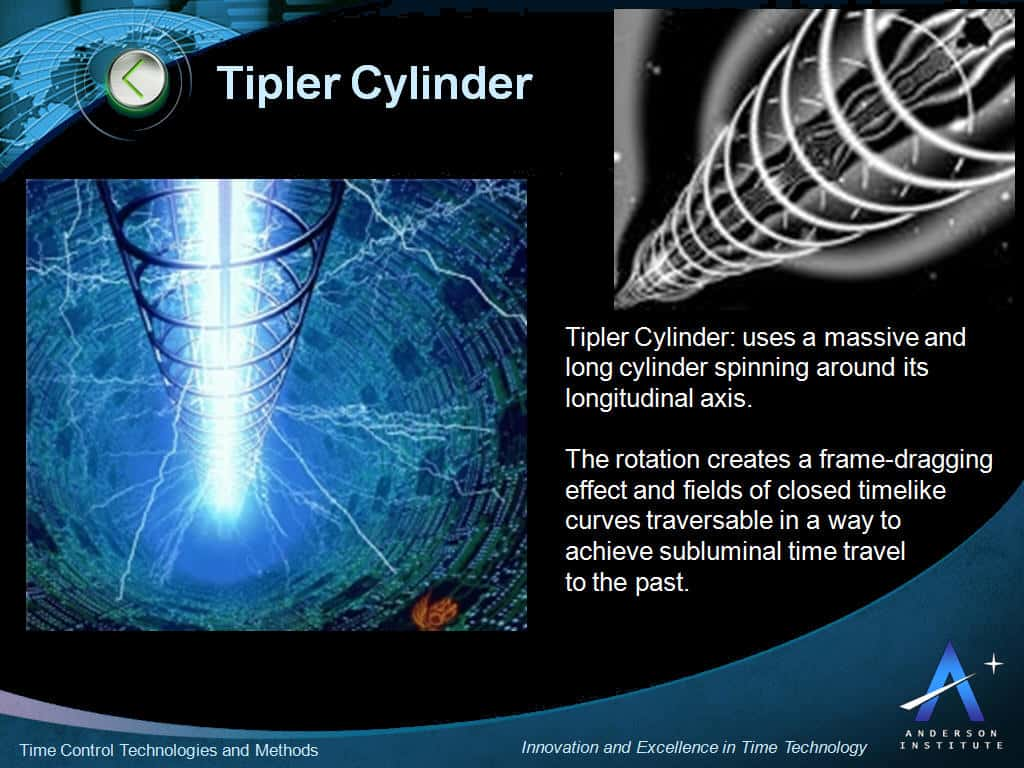
Une vue d'artiste d'un cylindre de Tipler construit par une civilisation technologiquement développée du futur. © Anderson Institute

Dans le film Contact, c'est une idée similaire qui est reprise pour créer un trou de ver puisque l'on voit d'imposants cerceaux en rotation ouvrant un passage vers l'étoile Végaétoile Véga.