au sommaire

La statistique de Bose et la quantification du rayonnement libre de Jordan
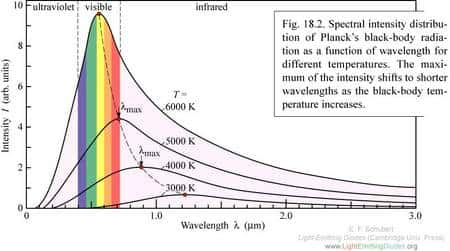
L'histoire de Satyeandra Nath Bose est remarquable. Jeune professeur à l'Université de Calcutta en Inde, il cherchait à préciser ses idées pour un cours sur la théorie des quanta de lumière d'EinsteinEinstein. Se trompant dans l'application des lois de la statistique de Maxwell-Boltzmann pour un gaz de particules, il redériva de façon presque purement quantique, et surtout très simplement, la loi du corps noir de PlanckPlanck !

Comprenant que son erreur était en fait une percée fondamentale, il décida de publier sa découverte. Les "referee" de l'époque rejetèrent l'article et Bose l'envoya en désespoir de cause à Albert Einstein.
Celui-ci comprit bien sûr instantanément sa valeur et il le traduisit en allemand et le fit publier lui-même en attirant de l'attention des chercheurs sur l'importance de ce travail.
Pour dériver la loi de Planck uniquement à partir de la formule de Planck, il fallait introduire une mystérieuse condition d'indiscernabilité pour les particules de lumière. Une hypothèse qui était en fait équivalente à l'erreur de calcul initiale de Bose, comme celui-ci l'avait parfaitement compris.
Aujourd'hui, les particules obéissant à la statistique de Bose-Einstein, comme on l'appelle, sont tout naturellement appelées des Bosons.

Fermi utilisera la même hypothèse d'indiscernabilité, mais combinée au principe d'exclusion de Pauliprincipe d'exclusion de Pauli, pour décrire les électronsélectrons. On aura alors ce qui est aujourd'hui connu sous le nom de statistique de Fermi-Dirac. En effet, Paul Dirac aura indépendamment la même idée.
La saga des quanta de Planck ne s'arrêta pas là.
Pascual Jordan, qui avait surtout reçu une formation de mathématicienmathématicien, est l'un des créateurs de la mécanique matricielle avec Heisenberg et Born. Alors que ces derniers préféraient attendre que la mécanique quantiquemécanique quantique se perfectionne, il est le premier à appliquer le formalisme de la mécanique matricielle aux équations de Maxwelléquations de Maxwell. Pour lui, la discontinuité de l'énergieénergie du rayonnement et la symétrie de comportement de la matièrematière et de la lumière ne pouvaient dire qu'une seule chose. La discontinuité du rayonnement devait avoir une origine similaire à la discontinuité des niveaux d'énergie dans l'atomeatome, et le formalisme mathématique qu'il avait développé dans deux articles avec Max Born et Heisenberg ne pouvait pas ne pas s'appliquer aux équations de Maxwell sous forme hamiltonienne. La loi de Planck devait pouvoir y trouver une dérivation beaucoup plus profonde.

On peut donc le considérer comme le fondateur de la théorie quantique des champs, même si les travaux les plus importants du domaine de 1925 à 1935 seront en réalité l'oeuvre de Pauli, Heisenberg et enfin Dirac et Fermi.
En décomposant à la manière de Rayleigh et Jeans le potentiel vecteur du champ électromagnétiquechamp électromagnétique, il quantifia ensuite les oscillateurs obtenus à l'aide des règles de la mécanique matricielle. Automatiquement, la mécanique statistique du système obéissait à la mystérieuse condition d'indiscernabilité que Bose avait introduite dans son article pour retrouver la loi de Planck.
Sur tous ces sujets, le livre d'Olivier Darrigol est une mine sur l'histoire des développements de la mécanique quantique. On consultera avec profit aussi les ouvrages de Françoise Balibard sur la démarche d'Einstein, liantliant de façon très importante ses travaux sur l'effet photo-électrique, la relativité restreinterelativité restreinte et le mouvementmouvement brownien.