Wheeler, Bekenstein et l'entropie en relativité générale

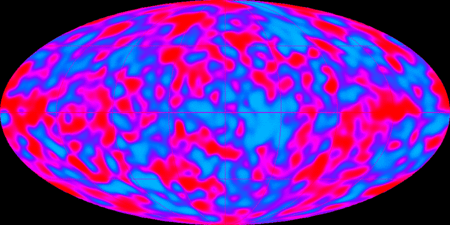
L'Univers étant conçu comme la totalité des choses, il est par définition ce que l'on appelle un système isolé dans le langage de la thermodynamique. Par conséquent, dans le cadre de la physique du XIX^ième siècle, il ne pouvait pas durer éternellement et devait se terminer par une mort thermodynamique. Bien sûr, avec la dérivation de la thermodynamique à partir de la mécanique statistique et donc des lois de la mécanique, un écoulement irréversible du temps ne pouvait être qu'une illusion et l'Univers, tôt ou tard, finirait par revenir à son état initial. C'était en effet une conséquence obligatoire du théorème de récurrence de Poincaré dans l'espace des phases d'un système mécanique.

L'entropieentropie et son accroissement inexorable pour un système fermé n'étaient donc qu'une illusion résultant de la résolutionrésolution trop faible dans l'espace et dans le temps des moyens d'observation d'un observateur humain. Une notion certes commode pour faire de la physique, mais non fondamentale. Boltzmann lui-même avait d'ailleurs introduit un modèle d'Univers où celui-ci était déjà dans un état d'équilibre thermodynamique, mais où localement des fluctuations faisaient croître ou décroître l'entropie et l'organisation, faisant croire aux observateurs nés localement d'une fluctuation d'entropie négative à une flèche du temps et à une loi d'accroissement de la complexité dans l'Univers.

La découverte de l'expansion de l'Univers allait changer quelque peu le tableau. En effet, un Univers même spatialement clos, mais dont le volumevolume était croissant, pouvait-il être considéré comme un système clos au sens thermodynamique?

Que penser aussi des solutions cosmologiques découvertes par Friedman et Lemaître dans lesquelles l'Univers passait par des phases d'expansion et de contraction ?

Dans les années 30 Richard Tolman avait pris le problème à bras le corps et avait montré que dans ces classes d'Univers simples, l'entropie de la matièrematière et du rayonnement ne pouvait que croître au cours du temps. Là aussi l'Univers ne pouvait être que difficilement éternel dans le passé et dans le futur.

Richard Tolman (1881-1948).

Après le milieu des années 50, John Wheeler, qui avait été un des artisans du programme de bombe thermonucléaire américain, se trouvait désoeuvré. Pourquoi ne pas utiliser ses connaissances sur la physique nucléaire et l'hydrodynamique des explosions thermonucléaires pour étudier les plus grandes explosions de tous les temps, les supernovaesupernovae et ce qui était encore à l'époque hypothétique : le Big BangBig Bang ?

En effet, selon Lemaître et sa théorie de l'atomeatome primitif, l'Univers avait commencé comme une sorte de particule élémentaireparticule élémentaire quantique puis avait «explosé » en se dégradant en un nombre important de particules. Gamow avait repris l'idée en introduisant un gazgaz de neutronsneutrons se désintégrant par radioactivitéradioactivité bêtabêta en protonsprotons et électronsélectrons. A Princeton, Wheeler était en plus le collègue d'EinsteinEinstein et il s'était laissé séduire par le programme unitaire de ce dernier cherchant à réduire l'ensemble de la physique, y compris les particules élémentaires, à une extension des équationséquations de la relativité généralerelativité générale.

Georges Gamow (1904-1968).

Le schéma général qui émergeait alors était celui d'un Univers primitif débutant dans un état où espace-tempsespace-temps et matière étaient profondément indifférenciés, sans charge, et ressemblant à une particule élémentaire/noyau subissant une désintégration radioactive en un gaz de neutrons chauds se désintégrant à leur tour en protons et électrons. La croissance du nombre de particules augmentant le nombre d'états initiaux disponibles pour l'énergieénergie de l'Univers, on passait donc d'un état d'entropie nulle ou quasi nulle à un état d'entropie croissante, une flèche du temps.

Il est intéressant d'ailleurs de noter que, tout comme Einstein, et pour des raisons de conditions aux limites naturelles des équations de la relativité générale ainsi qu'en liaison avec le principe de Mach, Wheeler adoptait l'idée d'un Univers clos, et donc cyclique.

Or, on peut montrer que la charge électrique globale d'un tel Univers est nécessairement nulle ! La « création » de l'Univers ne viole donc pas la loi de la conservation de la charge et se trouve tout naturellement en accord avec le postulatpostulat d'un gaz de neutrons initial de Gamow.

Yakov Zeldovitch (Crédit : Photo ca. 1950, courtesy Prof. V. I. Goldanskii)

En jouant avec ces idées, Wheeler et avec lui Yakov Zeldovitch, le co-créateur de la bombe H russe avec Sakharov lancé dans un programme similaire à celui de Wheeler, se rendirent compte d'une coïncidence surprenante mais fascinante. La géométrie interne de l'espace-temps d'une étoileétoile relativiste s'effondrant était identique à celle d'un Univers clos en expansion si l'on inversait le sens du temps !

La physique des étoiles à neutrons théorisées par Oppenheimer, Volkov et Snyder était donc un laboratoire naturel pour des modèles cosmologiques de type Big Bang. Mieux, c'était la physique des objets que Wheeler baptisera plus tard trou noirtrou noir qui devait contenir non seulement les secrets de la formation de l'Univers mais aussi ceux d'une théorie unitaire de l'espace-temps, de la matière et des interactions au sens d'Einstein.

Robert Geroch, un des grands spécialistes des théorèmes de singularités en relativité générale.

Wheeler était bien évidemment au courant du problème potentiel avec la croissance de l'entropie dans les Univers oscillants découvert par Tolman. Toutefois, la découverte des théorèmes de singularité en relativité générale par Penrose, Geroch, Ellis et surtout Hawking, avait montré qu'au moins en régime classique, les lois de la physique s'effondraient avec la singularité initiale de l'espace-temps présente dans tous les modèles cosmologiques. Wheeler avait de plus de bonnes raisons de croire à la non-conservation du nombre baryonique lorsqu'une étoile à neutronsétoile à neutrons s'effondrait en trou noir. Peut-être, après tout, la notion d'entropie elle-même ne résistait pas aux conditions infernales de températures et de courbure de l'espace-temps séparant deux phases d'expansion de l'Univers.

Le dictionnaire "physique des trous noirs et physique des modèles cosmologiques" possédait-il la réponse ?

Il discuta de ce problème avec un de ses jeunes étudiants, Jacob Bekenstein.

L'entropie est la mesure des différentes façons d'arranger les composants d'un système macroscopique dans un état thermodynamique donné. Il y a donc un nombre de micro-états possibles, par exemple les positions et les vitessesvitesses des particules d'un gaz parfaitgaz parfait, correspondant à ce même gaz dans un volume donné sous une certaine pressionpression et à une certaine température. Le logarithme de ce nombre est proportionnel à l'entropie du gaz. En considérant les moléculesmolécules d'un liquideliquide on aboutirait à la même constructionconstruction.
Prenons maintenant un glaçon et un verre d'eau chaude. Si l'on plonge le glaçon dans le verre celui-ci va fondre et la température du verre va baisser. Au final on calcul que l'entropie de ce système a augmenté, en plein accord avec les lois de la thermodynamique. "JetonsJetons maintenant ce verre dans un trou noir"  dit Wheeler.

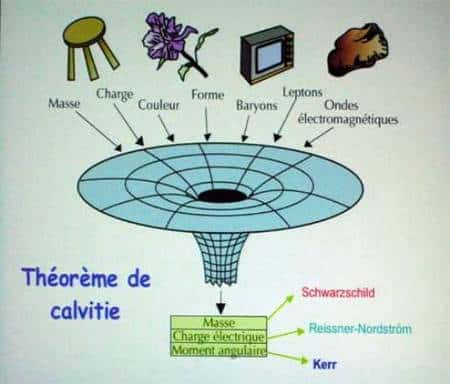
En traversant l'horizon et en s'approchant de la singularité, les forces de maréeforces de marée vont mettre en pièces les molécules d'eau, jusqu'aux protons eux-mêmes et au-delà !  Il ne restera alors plus qu'une solution de Schwarzschild décrivant un trou noir et ne dépendant que d'un seul paramètre : la massemasse de la matière tombée sous l'horizon. Dans cette description du trou noir en relativité générale classique, les micro-états de la matièreétats de la matière disparaissent dans la singularité pour ne plus en laisser qu'un. Au final, on a violé le second principe de la thermodynamiquesecond principe de la thermodynamique!

Une conclusion que Bekenstein n'était pas près à accepter, il chercha donc une échappatoire.

Jacob Bekenstein

Il remarqua que l'horizon des événementshorizon des événements d'un trou noir semblait rendre complètement indisponible l'information contenue dans un objet l'ayant traversé.

Or, selon la thermodynamique statistique et les analyses de Léon Brillouin faisant intervenir la théorie de l'information, l'entropie pouvait aussi se concevoir comme une mesure de la perte d'information, causée par le désordre d'un système, pour un observateur macroscopique. La croissance de l'horizon d'un trou noir, suite à son absorptionabsorption d'un objet, devait donc se traduire par un accroissement de l'entropie, par perte effective d'informations, pour un observateur extérieur.

D'une façon ou d'un autre, un trou noir devait enregistrer de l'information et l'on pouvait sauver le second principe si l'on acceptait de relier l'entropie S d'un trou noir à la surface de son horizon A par une fonction croissante S=f(A).

Par une analyse fine du taux de croissance de la surface d'un trou noir par absorption d'une particule quantique, dont la longueur d'ondelongueur d'onde de Compton était comparée au rayon de Schwarzschildrayon de Schwarzschild du trou noir dans lequel la particule tombait, il proposa une relation de proportionnalité entre S et A à un facteur près, en partie déterminé, mais dont la valeur exacte demandait à être précisée.