Réseaux de neurones et information mentale

Notre numéro de téléphone mobilemobile, un poème, une chanson ou encore les tables de multiplication laborieusement apprises durant notre enfance, voilà ce que l'on peut appeler de la « pure information mentale ».

Les réseaux de neurones. © Vitstudio, Shutterstock

Il s'agit donc de tout ce que notre cerveaucerveau, au cours de son long apprentissage, a mémorisé et rangé une fois pour toutes dans les méandres de ses connexions neuronales. Ici, aucun mouvement, nulle émotion, pas de subconscient. Neuf fois huit donnent 72, c'est mécanique, c'est immédiat. Cette information est précieusement rangée quelque part dans notre réseau neural, comme le sont des milliers de noms, des visages et toutes sortes d'éléments de connaissance sur lesquels notre raison s'appuie.

On appelle « neuroscience computationnelle » la branche des neurosciences qui s'intéresse aux modèles mathématiques de la cognitioncognition, et donc en premier lieu à ceux de l'information mentale. C'est dans ce champ de recherche que nous nous situons, et plus précisément dans les solutions offertes par les théories du connexionnisme et des réseaux de neurones.

Dans le réseau de neurones en (a) dont les connexions sont unidirectionnelles et pondérées, le signal se propage de la gauche (entrées) vers la droite (sorties). Le réseau récurrent en (b) contient des cycles, et les connexions peuvent y être pondérées ou simplement binaires, unidirectionnelles ou bidirectionnelles. © Télécom Bretagne

Types de réseaux de neurones

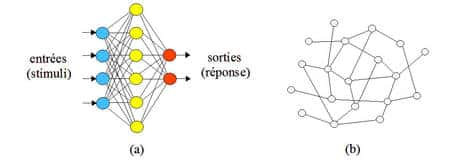
Les réseaux de neuronesneurones sont généralement classés en deux grandes familles :

• les réseaux non récurrents, figure (a) ci-dessus, dans lesquels un signal ne peut revenir vers le nœud d'où il est issu, même après modification par des traitements ultérieurs. Les connexions y sont nécessairement unidirectionnelles et sont appelées arcs (un terme emprunté au vocabulaire de la théorie des graphes). Ces arcs sont pondérés, les poids résultant de l'adaptation du réseau aux stimuli utilisés lors de l'apprentissage. Les poids sont donc les porteurs de l'information mémorisée. Un exemple bien connu, utilisé en reconnaissance automatique de caractères, en est le perceptron ;
• les réseaux récurrents qui contiennent des cycles (un autre terme de la théorie des graphes), lesquels autorisent des « retours de signal à l'envoyeur ». 

Pour ces réseaux récurrents, deux cas sont à considérer :

• lorsque les connexions y sont prédéfinies, auquel cas, comme pour les réseaux non récurrents, c'est leur pondération qui spécifie l'information ;
• lorsque chaque connexion, cette fois-ci non pondérée, peut exister ou non, comme sur la figure (b). Dans ce type de réseau, dit binairebinaire, l'information est exprimée par le graphe correspondant, c'est-à-dire par la connectivité.

Les deux grands courants des neurosciences computationnelles s'appuient sur ces deux visions de l'information mentale, la première la faisant porter par la force des liens (plasticité synaptique de nature analogiqueanalogique), la seconde par les motifs graphiques qui résultent de la présence ou de l'absence de connexions.