L’irruption de l’infini

Ces techniques développées par les comptablescomptables et les arpenteursarpenteurs constituent donc une préhistoire de l'arithmétique et de la géométrie. Que s'est-il donc passé de si spécial en Grèce, au Ve siècle avant notre ère, pour justifier que l'on fasse démarrer l'histoire à ce moment et non à un autre ?

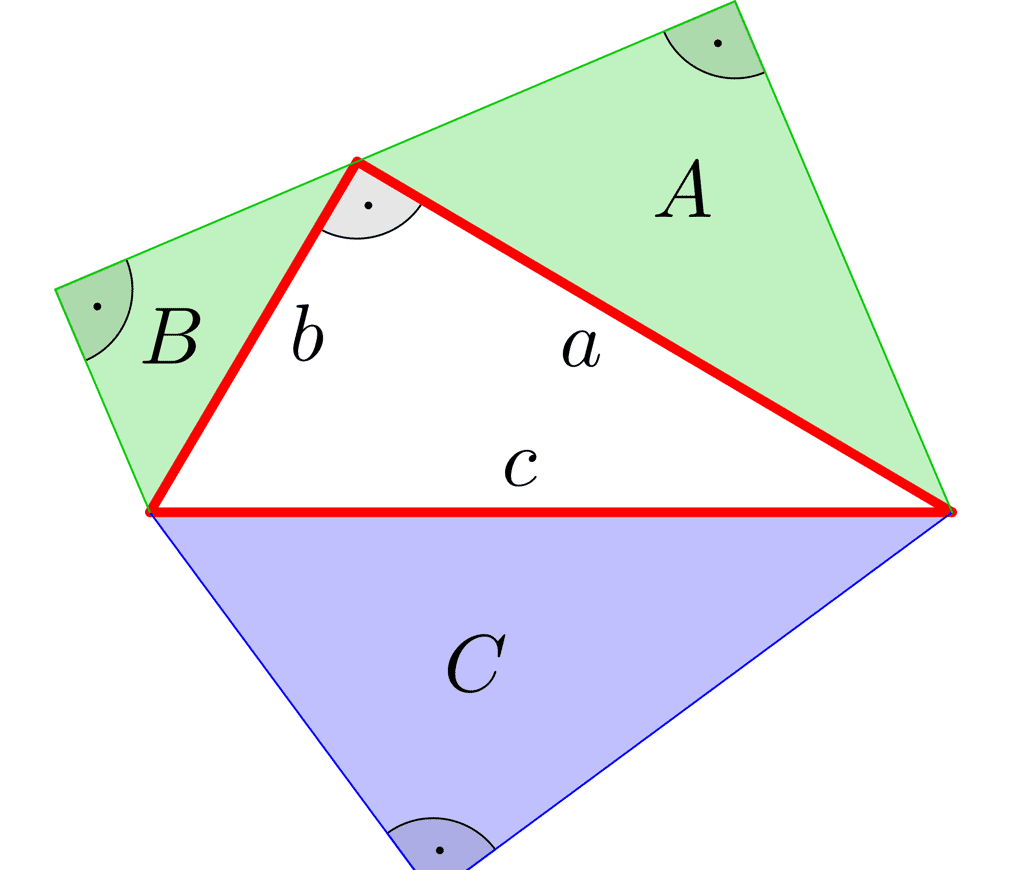
Le théorème de Pythagore. © Petrus3743, wikimedia commons, CC 4.0

Pour tenter de le comprendre, prenons l'exemple d'un problème résolu par un disciple de Pythagore dont le nom ne nous est pas parvenu : trouver un triangle rectangle et isocèle dont les trois côtés mesurent un nombre entier d'unités, disons un nombre entier de mètres. Comme le triangle est isocèle, ses deux petits côtés ont la même longueur : appelons-la x, et appelons y la longueur du grand côté, l'hypoténuse. Comme le triangle est rectangle, le nombre y² est, d'après le théorème de Pythagore, égal à x² + x². Le problème se ramène donc à celui de trouver deux nombres entiers x et y tels que : 2 × x² = y². Essayons toutes les possibilités dans lesquelles les nombres x et y sont inférieurs à 4 :

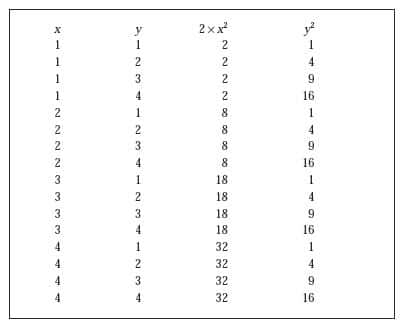
Dans tous ces cas, le nombre 2 × x² est différent de y². On peut poursuivre la recherche avec des nombres plus grands, et les pythagoriciens ont vraisemblablement cherché longtemps une solution à ce problème sans en trouver. Puis ils ont fini par se convaincre qu'une telle solution n'existait pas. Comment ont-ils pu se convaincre que ce problème n'avait pas de solution ? Naturellement pas en essayant tous les couples de nombres l'un après l'autre, car il en existe une infinité. On pourrait vérifier qu'aucun couple de nombres n'est une solution, jusqu'à mille, ou même jusqu'à un million, rien n'assurerait, avec certitude, qu'il n'existe pas de solution au-delà...

Essayons de reconstituer un cheminement possible de la pensée des pythagoriciens pour parvenir à ce résultat. Tout d'abord, quand on cherche une solution à ce problème,on peut se limiter à chercher une solution telle qu'au moins l'un des nombres x et y soit impair, car si le couple, x = 202, y = 214, par exemple, était une solution, alors en divisant les deux nombres par 2, on obtiendrait une autre solution, x = 101, y = 107, dont au moins l'un des nombres est impair. Plus généralement, en partant d'une solution quelconque et en divisant les deux nombres par 2, éventuellement plusieurs fois, on finirait par obtenir une solution dans laquelle au moins l'un des nombres est impair. Si le problème avait une solution, il en aurait donc également une dans laquelle l'un des nombres x et y est impair.

La seconde idée est de classer les couples de nombres en quatre ensembles :

- les couples dans lesquels les deux nombres sont impairs,
- ceux dans lesquels le premier nombre est pair et le second impair,
- ceux dans lesquels le premier nombre est impair et le second pair,
- et enfin ceux dans lesquels les deux nombres sont pairs. Muni de ces deux idées, on peut montrer, par quatre arguments séparés, qu'aucun de ces ensembles ne contient de solution dans laquelle au moins l'un des nombres x et y est impair, donc que le problème n'a pas de solution dans laquelle au moins l'un des nombres est impair, donc que le problème n'a pas de solution du tout.

Commençons par le premier ensemble : une solution dans laquelle x et y sont l'un et l'autre impairs est impossible, car si le nombre y est impair, le nombre y² l'est également et il n'a aucune chance d'être égal à 2 × x², nécessairement pair. Cet argument permet aussi d'éliminer le deuxième cas, dans lequel x est pair et y impair. Le quatrième cas s'élimine de lui-même car, par définition, il ne peut pas contenir de couples dans lequel au moins l'un des nombres est impair. Reste le troisième, dans lequel x est impair et y est pair. Dans ce cas, la moitié de 2 × x² est impaire, alors que celle de y² est paire : ces deux nombres ne peuvent pas être égaux.

Ce résultat - un carré ne peut être le double d'un autre carré - obtenu par les pythagoriciens il y a plus de vingt-cinq siècles, tient encore aujourd'hui une place importante dans les mathématiques. Il montre que, quand on dessine un triangle rectangle isocèle dont le petit côté mesure 1 m, la longueur de l'hypoténuse, mesurée en mètres, est un nombre, √2 , qui vaut un peu plus de 1,414, mais qui ne peut pas être obtenu en divisant deux nombres entiers y et x l'un par l'autre. La géométrie fait donc apparaître des nombres que l'on ne peut pas obtenir à partir des nombres entiers avec les quatre opérations : l'addition, la soustraction, la multiplication et la division.

Cette remarque a amené, plusieurs siècles plus tard, les mathématiciensmathématiciens à construire de nouveaux nombres, les « nombres réels », mais les pythagoriciens ne sont pas allés jusque-là : ils n'étaient pas prêts à abandonner le caractère central qu'ils supposaient aux nombres entiers, et ils ont plutôt vécu leur découverte comme une catastrophe que comme une incitation à aller plus loin.

Ce problème n'est pas uniquement révolutionnaire par ses implications pour les mathématiques futures. Il l'est aussi par sa nature et par la méthode employée pour le résoudre. Tout d'abord, par comparaison avec celui de la tablette mésopotamienne qui consiste à diviser 1 152 000 mesures de grain par 7 mesures, le problème des pythagoriciens est plus abstrait. Celui des Mésopotamiens concerne des nombres de mesures de grain, celui des pythagoriciens concerne des nombres tout court. De même, dans sa forme géométrique, le problème ne concerne pas une surface agricole triangulaire, mais un triangle. Cette étape d'abstraction, qui consiste à passer du champ triangulaire au triangle ou du nombre de mesures de grain au nombre, est moins anodine qu'il paraît. En effet, la taille d'un champ ne peut pas dépasser quelques kilomètres. Si le problème concernait un champ triangulaire, et non un triangle abstrait, on pourrait le résoudre en essayant toutes les solutions dans lesquelles x et y sont inférieurs à 10 000. Or, à la différence d'un champ triangulaire, rien n'empêche un triangle de mesurer un million ou un milliard de kilomètres.

La grande révolution du Ve siècle avant notre ère consiste donc en la distance mise entre les objets mathématiques, qui sont abstraits, et les objets concrets de la nature, même quand les objets mathématiques sont construits par abstraction à partir des objets concrets.

Cette distance entre les objets mathématiques et les objets de la nature a incité certains à penser que les mathématiques ne permettaient pas de décrire les objets de la nature. Cette thèse a été vivace jusqu'à l'époque de GaliléeGalilée, c'est-à-dire au début du XVIIe siècle, où elle a été balayée par les succès de la physique mathématique. Elle est encore présente, à l'état résiduel, dans certains discours qui dénient toute pertinence aux mathématiques dans le domaine des sciences humaines. Ainsi, selon Marina Yaguello, le rôle des mathématiques en linguistique est de « déguise[r] son complexe de "science humaine", donc fondamentalement inexact, sous des formules ».

Ce changement dans la nature des objets étudiés - qui, depuis cette révolution, sont des figures géométriques et des nombres sans une relation nécessaire avec les objets concrets - a amené une révolution dans la méthode utilisée pour résoudre les problèmes mathématiques. Encore une fois, comparons la manière de résoudre les problèmes de la tablette mésopotamienne et des pythagoriciens. Le premier est résolu en effectuant un calcul : une simple division. Pour résoudre le second, en revanche, il est nécessaire de construire un raisonnement.

Pour faire une division, il suffit d'appliquer un algorithme, que l'on apprend à l'école primaire et dont les Mésopotamiens connaissaient des analogues. Mais, pour construire le raisonnement des pythagoriciens, aucun algorithme connu ne prescrit de classer les couples en quatre ensembles. Les pythagoriciens ont dû faire preuve d'imagination pour parvenir à cette idée. On peut penser qu'un premier pythagoricien a compris que le nombre y ne pouvait pas être impair puis, quelques semaines ou quelques mois plus tard, un autre a fait progresser le problème en découvrant que x non plus ne pouvait être impair. Et puis le problème est peut-être resté bloqué là pendant des mois ou des années avant qu'un autre trouve encore une idée. Quand un Mésopotamien attaque une division, il sait qu'il va aboutir et il peut même évaluer a priori le temps que cette division lui prendra. En revanche, quand un pythagoricien attaque un problème d'arithmétique, il ne peut pas savoir combien de temps il mettra pour trouver un raisonnement qui permette de le résoudre, ni même s'il en trouvera un jour.

Les écoliers se plaignent parfois que les mathématiques sont difficiles : il faut avoir de l'imagination, il n'existe pas de méthode systématique pour résoudre les problèmes. Ils ont raison, et les mathématiques sont encore plus difficiles pour les mathématiciens professionnels : certains problèmes sont restés sans solution pendant des décennies, voire des siècles, avant que quelqu'un les résolve. Il n'y a rien d'extraordinaire à « sécher » longtemps sur un problème mathématique: les mathématiciens eux aussi « sèchent », parfois longtemps, avant de résoudre un problème. En revanche, on n'imagine pas de « sécher » des heures sur une division, puisqu'il suffit d'appliquer l'algorithme bien connu.

Comment ce changement dans la nature des objets étudiés a-t-il amené ce changement dans la méthode utilisée pour résoudre les problèmes - ce passage du calcul au raisonnement, qui caractérise les mathématiques grecques ? Qu'est-ce qui fait que le problème des pythagoriciens ne peut pas être résolu par un calcul ? Comparons-le encore une fois au problème de la tablette mésopotamienne. Ce dernier concerne un objet particulier, un grenier rempli de grain, dont la taille est connue. Dans le problème des pythagoriciens, en revanche, le triangle n'est pas connu: c'est ce que l'on cherche. Ce problème ne concerne donc pas un triangle particulier mais, potentiellement, tous les triangles possibles. En outre, comme il n'existe pas de limite à la taille d'un triangle, le problème concerne simultanément une infinité de triangles. Ce changement dans la nature des objets mathématiques s'accompagne donc d'une irruption de l'infini dans les mathématiques : c'est cette irruption qui a rendu un changement de méthode nécessaire et a demandé de substituer le raisonnement au calcul. Comme on l'a déjà remarqué, si le problème ne concernait qu'un nombre fini de triangles, par exemple tous les triangles dont les côtés mesurent moins de 10 000 mètres, on pourrait s'en tirer par un calcul qui consiste à essayer tous les couples de nombres jusqu'à 10 000. Ce calcul est certes laborieux si on le fait à la main, mais il est systématique. Ce passage du calcul au raisonnement a été retenu comme l'acte de naissance des mathématiques, en Grèce, au Ve siècle avant notre ère.