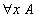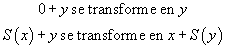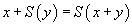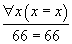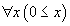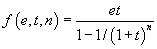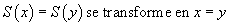Le raisonnement

Pourquoi ne pouvons nous pas nous contenter du calcul et avons nous eu besoin de passer du calcul au raisonnement ? Parce que, outre les propositions telles que 9 + 57 = 66, nous voulons également établir des propositions générales, qui parlent non d'un nombre particulier mais de tous les nombres à la fois, par exemple

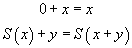
La première proposition peut s'établir avec les règles ci-dessus.
Dans l'expression 0 + x, nous ne connaissons pas x, mais c'est un certain nombre de bâtons qu'on peut mettre dans une boîte, et le terme

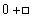
se transforme par la première règle en

sans ouvrir la boîte. Mais ce n'est pas le cas de toutes les propositions générales, en particulier la seconde proposition ne peut pas s'établir ainsi. Tout ce qu'on peut faire avec le terme

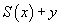
c'est le transformer en

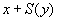
Et avec le terme

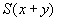
on ne peut rien faire. Cette proposition est un exemple de propositions qu'on peut démontrer en arithmétique uniquement en utilisant le principe de récurrence. On préfère donc oublier cet aspect de calcul et utiliser un outil plus puissant : la déduction. Ces règles de calcul sont supprimées et deviennent des axiomes

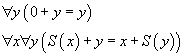
En démonstration automatique, on en vient à se demander si c'est une bonne idée de remplacer ainsi les règles de calcul par des axiomes.

Un programme de démonstration automatique est un programme auquel on peut poser une question, par exemple « est ce que

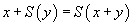
et qui répond oui, éventuellement en donnant une démonstration du théorème. Ce type de programmes ne permet pas, aujourd'hui, de démontrer des théorèmes difficiles, mais il s'avère que dans beaucoup d'applicationsapplications concrètes en informatique, il est utile de pouvoir démontrer automatiquement des propositions comme celle-ci, même si leurs démonstrations sont triviales du point de vue mathématique.

On veut aussi pouvoir demander à ce type de programmes « est ce que 9 + 57 = 66 ? », et on se trouve dans une situation paradoxale, où pour établir cette proposition, le programme est obligé d'en chercher une démonstration en arithmétique. On a donc un programme qui, certes sait faire des démonstrations pour établir des phrases générales, mais qui, quand on lui demande d'effectuer un simple calcul, situation où un ordinateurordinateur devrait avoir une certaine facilité, essaye de démontrer cette proposition par tous les moyens possibles. Il y a beaucoup de manières de démontrer cette proposition, par exemple en utilisant la commutativité de l'addition, on peut se ramener à la question « est ce que 57 + 9 = 66 ? », en utilisant certains des axiomes on peut se ramener à la question « est ce que 10 + 56 = 66 ? ». On peut aussi se ramener à la question « est ce que 8 + 58 = 66 ? » et cette voie de recherche est la bonne, puisque c'est elle qui, en quelque sorte, simule le calcul et mène à la question « est ce que 0 + 66 = 66 ? » qui peut être résolue par l'un des axiomes, mais entre-temps on explore toutes les autres voies qui mènent à des impasses, comme celle qui consiste à permuter les deux membres à l'infini.