au sommaire

    Au coeur de la géométrie projective. © Tpsdave - Domaine public

    Au coeur de la géométrie projective. © Tpsdave - Domaine public

    Au cœur de la géométrie projective se trouve le théorème de Pappus. Voyons ici ses applications.

    Application du théorème de Pappus. © HB licence Creative Commons paternité – partage à l’identique 3.0 (non transposée).

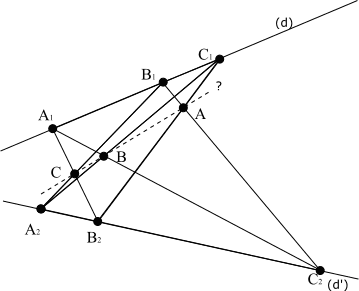
    Application du théorème de Pappus. © HB licence Creative Commons paternité – partage à l’identique 3.0 (non transposée).

    Principe du théorème de Pappus

    Prenons deux rangées de trois oliviersoliviers. Les trois oliviers de chaque rangée sont alignés, mais les rangées ne sont pas parallèles. Pouvons-nous planter trois nouveaux oliviers pour obtenir dix rangées de trois arbresarbres ?

    Nous résolvons le problème en utilisant le théorème de Pappus. Ce théorème stipule que si nous relions par des droites chacun des trois points (A1, B1, C1 quelconques) d'une première droite à deux points (A2, B2, C2, quelconques) d'une seconde droite, alors les points d'intersection (A, B, C) de ces droites sont alignés.

    Le fermier résout son problème d'alignement en transplantant l'olivier B1 le long de sa rangée de façon que la droite B1, B, B2 constitue la 10e rangée. Démontré en 340, le théorème de Pappus, qui ne fait intervenir aucune mesure de longueur ou d'angle, est typique de la géométrie projective.