Les fondateurs de la géométrie et les mathématiciens grecs

Les mathématiciensmathématiciens grecs les plus célèbres sont probablement Pythagore et EuclideEuclide, mais le véritable père de la géométrie est ThalèsThalès.

Les pyramides de Gizeh. © Walkerssk - Shutterstock

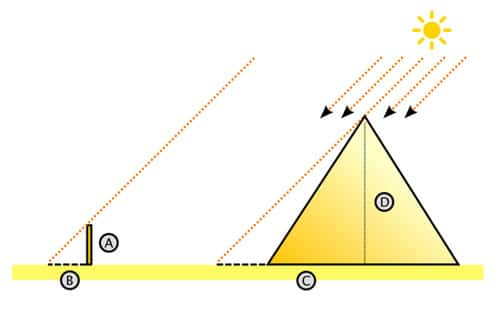
Pythagore, Euclide et Thalès sont les représentants de la géométrie. Un des célèbres calculs est celui de Thalès, concernant la pyramide de Khéops. Quand le soleil était dans la bonne position, Thalès déduisait de la longueur de l'ombre (en pointillés), la hauteur de la pyramide (D). Ici, D = (A x C) : B. C étant égal à la longueur de l'ombre plus la longueur de la demi-base de la pyramide. © Dake licence Creative Commons paternité – partage à l’identique 3.0 (non transposée).

Ils ne sont plus enseignés aujourd'hui, mais les « Éléments d'Euclide » feraient resurgir des souvenirs scolaires chez nos arrière-grands-parents. Bien qu'Euclide soit souvent considéré comme le père de la géométrie, cette distinction revient en toute équité à Thalès (640-546 av. J.-C.) qui étudia la géométrie trois siècles avant Euclide.

Thalès et le calcul de la hauteur de la pyramide de Khéops

Bien que nous n'ayons aucun document datant de l'époque de Thalès, la tradition orale a transmis un bon nombre d'histoires : la plus célèbre est la méthode de calcul de la hauteur de la pyramide de Khéops, construite il y a environ 4.600 ans.

Nous ne connaissons pas dans le détail les méthodes géométriques utilisées par les Égyptiens pour construire les pyramides et la détermination de la hauteur totale d'une pyramide a longtemps été une énigme. Thalès remarqua qu'à un certain moment du jour, la longueur de l'ombre d'un objet était égale à sa taille. À cette heure du jour (repérée par la position du soleil dans le ciel), il mesure la longueur de l'ombre de la pyramide à partir de sa base. Puis il ajoute la moitié de la longueur de la base et détermina ainsi la hauteur de la pyramide.

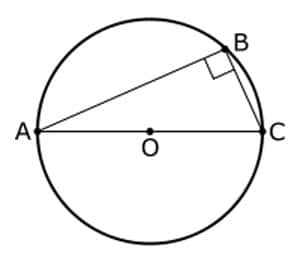
Théorème de Thalès sur le cercle. © Domaine public

Théorème de Thalès et triangle isocèle

On attribue également à Thalès la découverte que le diamètre d'un cercle coupe celui-ci en deux parties d'aires égales, et que dans un triangle isocèle (un triangle ayant deux côtés égaux) les angles opposés aux côtés égaux sont aussi égaux. Aujourd'hui, même quelqu'un qui éprouve une grande aversion pour les mathématiques ne serait pas tellement surpris par ces « découvertes » : elles lui sembleraient plus des remarques de bon sens que de puissants résultats mathématiques.

Toutefois, du temps de Thalès, ces avancées étaient remarquables dans la mesure où les conclusions de Thalès portaient sur tous les cercles et tous les triangles isocèles. Cette généralisation déductive était un nouveau moyen de penser les mathématiques, un moyen détaché de toute considération pratique portant sur des cercles ou des triangles particuliers. Ainsi, Thalès inventa un mode de raisonnement dont toutes les mathématiques modernes sont issues.

Il transforma les mesures de la géométrie en l'étude des invariants : les propriétés des cercles ou des triangles isocèles qui ne dépendent pas de la taille de ces objets. Il existe une multitude de diamètres de cercles, mais ils découpent tous le cercle en deux parties égales. Toutes les branches de la géométrie utilisent de tels « invariants ».

Pour rappel, exemple de formulation du théorème de Thalès : « soit un triangle ABC et deux points D et E (respectivement entre A et B et entre A et C) formant en les joignant une ligne parallèle à BC. Alors AD/AB = AE/AC = DE/BC ».