au sommaire
Vous trouverez des jeux simples et toujours concrets, qui ont été testés auprès d'enfants accompagnés d'un adulte possédant les connaissances requises. Ces jeux incitent à l'observation de la nature, à l'action par des tracés à la corde (au sol) ou au compas (sur une feuille) puis à la réflexion et à l'interprétation des résultats.

Ils prouvent d'une façon irréfutable l'existence du nombre d'or dans la nature et pour ça, il faut aller jusqu'au dernier jeu. C'est une des approches possibles du nombre d'or, elle n'est faite ici que par l'intermédiaire de suites de grandeurs concrètes, dites suites de Fibonacci. Un deuxième article de 2004 du même auteur est d'une toute autre approche et il arrive étonnamment aux mêmes résultats graphiques, au nombre d'or.
Tout internaute de tout âge y trouvera sûrement beaucoup d'intérêt.

Le nombre d'or dans la nature ou l'équilibre parfait
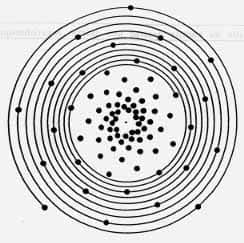
Observez cette branche de sapinsapin et les aiguilles qu'elle porteporte. Certaines aiguilles sont tombées mais en laissant une trace sur la tige. Les aiguilles ont-elles poussé au plus grand des hasards ou ont-elles obéi à une loi naturelle de répartition qui se retrouve sur toutes les branches de sapin ? Ce dossier vous donnera la solution pour le cœur d'une gerbera et d'une marguerite mais pour le sapin, c'est pour d'autres jeux.
À lire aussi sur Futura :
- L'arithmétique et les plantes
- 15 images de fractales renversantes
- Kézako : quel est le point commun entre un ananas, des lapins et la tour de Pise ?