au sommaire
Cet article revient sur les problèmes posés par la détermination du rayon terrestre par ÉratosthèneÉratosthène : mesure de l'angle et mesure de la distance terrestre qui conduisent à s'interroger sur la précision supposée de cette expérience.

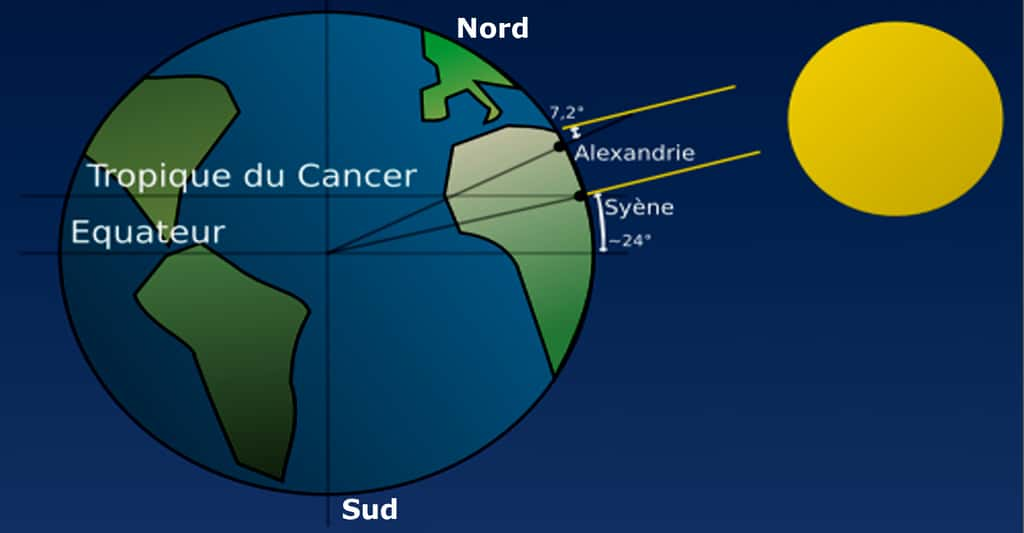
Suite à mon article (« Histoire des sciences : une expérience pédagogique en seconde », BUP n° 843, avril 2002 - http://www.cnam.fr/hebergement/udp/), il me semble opportun de revenir sur la mesure d'Ératosthène (v 284 - v 192 av. J.-C.) qui figure au programme de cette classe et que les manuels présentent à peu près comme ceci : ÉRATOSTHÈNE, qui admet la sphéricité de la Terre, en calcule le rayon croyant que Syène (aujourd'hui Assouan) se trouve sur le même méridien qu'Alexandrie. Le jour du solstice d'été dans cette dernière ville, il constate à midi que le rayon lumineux passant par l'extrémité de l'ombre d'un obélisque fait un angle égal à un cinquantième du tour du cercle (7°12'), alors que les rayons solaires tombent à Syène en éclairant le fond des puits. Faisant l'hypothèse que ces rayons arrivent parallèles sur la Terre, il en déduit que la distance Syène-Alexandrie (5 000 stades) équivaut au cinquantième du méridien, ce qui entraîne donc pour la circonférence terrestre la valeur de 250 000 stades.
Si la mesure angulaire de l'astronomeastronome (7°12') semble convenable (Syène est à 24°5'de latitudelatitude Nord et Alexandrie à 31°12' de latitude Nord), sa supposition que les deux villes sont sur le même méridien est erronée (1) Mais cet écart n'affecte pas beaucoup l'ordre de grandeurordre de grandeur du résultat.
Une deuxième remarque concerne le « stade », unité associée normalement aux longueurs des stades d'Olympie ou de Delphes : cependant, certains érudits suggèrent qu'ÉRATOSTHÈNE aurait pu utiliser une autre grandeur avec cette appellation. En fonction donc de l'étalon réellement employé, il a dû attribuer à la circonférence de la Terre une longueur oscillant entre 39 700 et 46 600 de nos actuels kilomètres, valeur d'une remarquable précision.